
【题目】已知数列{![]() }中,
}中,![]() ,且
,且![]() 对任意正整数都成立,数列{
对任意正整数都成立,数列{![]() }的前n项和为Sn。
}的前n项和为Sn。
(1)若![]() ,且
,且![]() ,求a;
,求a;
(2)是否存在实数k,使数列{![]() }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若![]() 。
。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
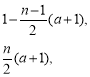
![]()
【解析】
试题分析:(1)![]() 时,
时,![]() ,由等差数列定义知数列
,由等差数列定义知数列![]() 是等差数列,由
是等差数列,由![]() 可得
可得![]() ,解得
,解得![]() ,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{
,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{![]() }是公比不为1,所以
}是公比不为1,所以![]() 不为等差中项,只需讨论
不为等差中项,只需讨论![]() 与
与![]() 为等差中项:若
为等差中项:若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得:![]() ,解得
,解得![]() (舍1);
(舍1);![]() ;同理若
;同理若![]() 为等差中项,
为等差中项,![]() (3)
(3)![]() 则
则![]() ,
,![]() ,从而
,从而![]() ,所以求和时要重新组合,每两项作为一组,先求
,所以求和时要重新组合,每两项作为一组,先求![]() 是偶数时,
是偶数时,![]()
![]()
![]() ,再求
,再求![]() 是奇数时,
是奇数时,![]()
![]()
![]()
![]()
![]() ,
,
试题解析:(1)![]() 时,
时,![]() ,
,![]() ,所以数列
,所以数列![]() 是等差数列 1分
是等差数列 1分
此时首项![]() ,公差
,公差![]() ,数列
,数列![]() 的前
的前![]() 项和是
项和是![]() 3分
3分
故![]() ,即
,即![]() ,得
,得![]() ; 4分
; 4分
(没有过程,直接写![]() 不给分)
不给分)
(2)设数列![]() 是等比数列,则它的公比
是等比数列,则它的公比![]() ,所以
,所以![]() ,
,![]() ,
,![]() 6分
6分
①若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,解得:
,解得:![]() ,不合题意;
,不合题意;
②若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得:![]() ,
,
解得![]() (舍1);
(舍1);![]() ;
;
③若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得:![]() ,
,
解得![]() ;
;![]() ; 9分
; 9分
综上可得,满足要求的实数![]() 有且仅有一个,
有且仅有一个,![]() ; 10分
; 10分
(3)![]() 则
则![]() ,
,
![]() ,
,![]() , 12分
, 12分
当![]() 是偶数时,
是偶数时,
![]()
![]()
![]() ,
,
当![]() 是奇数时,
是奇数时,
![]()
![]()
![]()
![]()
![]() ,
,![]() 也适合上式, 15分
也适合上式, 15分
综上可得,![]()
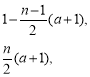
![]() . 16分
. 16分


科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知数列![]() (
(![]() ,
, ![]() )满足
)满足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的取值范围;
的取值范围;
(2)设集合![]() .
.
①若![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
②是否存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() ?若存在,请求出实数
?若存在,请求出实数![]() ,
, ![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获纯利多少元?
已知: ![]() x
x ![]() =280,
=280, ![]() y
y ![]() =45309,
=45309, ![]() xiyi=3487,
xiyi=3487, ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2 (a为实常数).
(1)当a=﹣4时,求函数f(x)的单调区间;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数;
(3)若 a>0,且对任意的x1 , x2∈[1,e],都有|f(x1)﹣f(x2)| ![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 。
。
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值。
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x![]() 时,
时,
恒有f(x)>g(x)成立。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线y2=2x的焦点为F,过点M( ![]() ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,|BF|=2,则△BCF和△ACF的面积之比为 .
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,|BF|=2,则△BCF和△ACF的面积之比为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法,对于求一个n次多项式函数fn(x)=anxn+an﹣1xn﹣1+…+a1x+a0的具体函数值,运用常规方法计算出结果最多需要n次加法和 ![]() 乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5﹣x4+3x3﹣5x当x=3时的值时,最先计算的是( )
乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5﹣x4+3x3﹣5x当x=3时的值时,最先计算的是( )
A.﹣5×3=﹣15
B.0.5×3+4=5.5
C.3×33﹣5×3=66
D.0.5×36+4×35=1336.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知☉O1与☉O2相交于A,B两点,过点A作☉O1的切线交☉O2于点C,过点B作两圆的割线,分别交☉O1、☉O2于点D、E,DE与AC相交于点P.若AD是☉O2的切线,且PA=6,PC=2,BD=9,则AB的长为____.

查看答案和解析>>
科目:高中数学 来源: 题型:
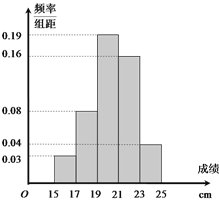
【题目】某班![]() 名学生在一次坐位体前屈测试中,成绩全部介于
名学生在一次坐位体前屈测试中,成绩全部介于![]() 与
与![]() 之间,将测试结果按如下方式分成五组:第一组
之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(Ⅰ)若成绩大于或等于![]() 且小于
且小于![]() 认为良好,求该班在这次坐位体前屈测试中成绩良好的人数;
认为良好,求该班在这次坐位体前屈测试中成绩良好的人数;
(Ⅱ)若成绩之差的绝对值大于![]() 认为两位学生的身体韧度存在明显差异.现从第一、五组中随机取出两个成绩,求这两位学生的身体韧度存在明显差异的概率.
认为两位学生的身体韧度存在明显差异.现从第一、五组中随机取出两个成绩,求这两位学生的身体韧度存在明显差异的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com