
【题目】数列![]() 的前
的前![]() 项和记为
项和记为![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,
上, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,
, ![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,求
项和,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 在直线
在直线![]() 上可得,
上可得, ![]() ,所以
,所以![]() ,两式相减得
,两式相减得![]() 为等比数列,从而得出
为等比数列,从而得出![]() 的通项公式;(2)求出
的通项公式;(2)求出![]() ,利用分组求和法以及等差数列的求和公式与等比数列的求和公式可得出
,利用分组求和法以及等差数列的求和公式与等比数列的求和公式可得出![]() .
.
试题解析:(1)由题知![]() ,所以
,所以![]() ,两式相减得
,两式相减得
![]() ,又
,又![]() ,
,
所以![]() 是以1为首项,4为公比的等比数列.
是以1为首项,4为公比的等比数列.
![]()
(2)![]() ,
, ![]() ,
,
所以![]()
![]() .
.
【方法点晴】本题主要考查等比数列的定义与通项、等差数列的求和公式与等比数列的求和公式以及利用“分组求和法”求数列前![]() 项和,属于中档题. 利用“分组求和法”求数列前
项和,属于中档题. 利用“分组求和法”求数列前![]() 项和常见类型有两种:一是通项为两个公比不相等的等比数列的和或差,可以分别用等比数列求和后再相加减;二是通项为一个等差数列和一个等比数列的和或差,可以分别用等差数列求和、等比数列求和后再相加减.
项和常见类型有两种:一是通项为两个公比不相等的等比数列的和或差,可以分别用等比数列求和后再相加减;二是通项为一个等差数列和一个等比数列的和或差,可以分别用等差数列求和、等比数列求和后再相加减.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】一条光线经过P(2,3)点,射在直线l:x+y+1=0上,反射后穿过点Q(1,1).
(1)求入射光线的方程;
(2)求这条光线从P到Q的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
(2)若![]() 且关于
且关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围;
的取值范围;
(3)设各项为正的数列![]() 满足:
满足: ![]() 求证:
求证: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

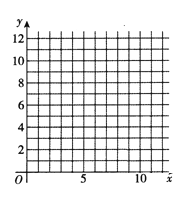
(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线![]() 的右下方的概率.
的右下方的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:三棱锥![]() 中,侧面
中,侧面![]() 垂直底面,
垂直底面, ![]() 是底面最长的边;图1是三棱锥
是底面最长的边;图1是三棱锥![]() 的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥
的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥![]() 的直观图的一部分,其中点
的直观图的一部分,其中点![]() 在
在![]() 平面内.
平面内.
(Ⅰ)请在图2中将三棱锥![]() 的直观图补充完整,并指出三棱锥
的直观图补充完整,并指出三棱锥![]() 的哪些面是直角三角形;
的哪些面是直角三角形;![]()
![]()
(Ⅱ)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值;
的值;
(Ⅲ)求点![]() 到面
到面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图像如图所示,则下列结论中一定成立的是( )
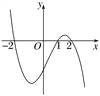
A. 函数f(x)有极大值f(2)和极小值f(1) B. 函数f(x)有极大值f(-2)和极小值f(1)
C. 函数f(x)有极大值f(2)和极小值f(-2) D. 函数f(x)有极大值f(-2)和极小值f(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com