
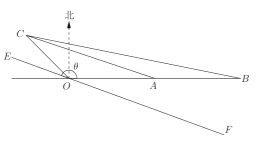
【题目】如图,![]() 为信号源点,
为信号源点,![]() 、
、![]() 、
、![]() 是三个居民区,已知
是三个居民区,已知![]() 、
、![]() 都在
都在![]() 的正东方向上,
的正东方向上,![]() ,
,![]() ,
,![]() 在
在![]() 的北偏西45°方向上,
的北偏西45°方向上,![]() ,现要经过点
,现要经过点![]() 铺设一条总光缆直线
铺设一条总光缆直线![]() (
(![]() 在直线
在直线![]() 的上方),并从
的上方),并从![]() 、
、![]() 、
、![]() 分别铺设三条最短分支光缆连接到总光缆
分别铺设三条最短分支光缆连接到总光缆![]() ,假设铺设每条分支光缆的费用与其长度的平方成正比,比例系数为1元/
,假设铺设每条分支光缆的费用与其长度的平方成正比,比例系数为1元/![]() ,设
,设![]() ,(
,(![]() ),铺设三条分支光缆的总费用为
),铺设三条分支光缆的总费用为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】如图,已知在长方体![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上的一个动点,平面
上的一个动点,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,给出下列命题:
,给出下列命题:
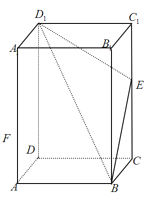
①四棱锥![]() 的体积为
的体积为![]() ;
;
②存在唯一的点![]() ,使截面四边形
,使截面四边形![]() 的周长取得最小值
的周长取得最小值![]() ;
;
③当![]() 点不与
点不与![]() ,
,![]() 重合时,在棱
重合时,在棱![]() 上均存在点
上均存在点![]() ,使得
,使得![]() 平面
平面![]()
④存在唯一一点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]()
其中正确的命题是_____________(填写所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上所有点横坐标缩短为原来的
上所有点横坐标缩短为原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的参数方程和
的参数方程和![]() 的取值范围;
的取值范围;
(2)求![]() 中点
中点![]() 的轨迹的参数方程.
的轨迹的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.
,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.
(1)求曲线C的方程;
(2)设不经过点![]() 的直线l与曲线C相交于A,B两点,直线QA与直线QB的斜率均存在且斜率之和为-2,证明:直线l过定点.
的直线l与曲线C相交于A,B两点,直线QA与直线QB的斜率均存在且斜率之和为-2,证明:直线l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
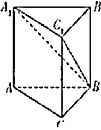
【题目】我国古代数学名著《九章算术》中有这样一些数学用语,“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,而“阳马”指底面为矩形,且有一侧棱垂直于底面的四棱锥.现有一如图所示的堑堵,![]() ,若
,若![]() ,当阳马
,当阳马![]() 体积最大时,则堑堵
体积最大时,则堑堵![]() 的外接球体积为( )
的外接球体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com