
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1且关于直线l对称.
的半径为1且关于直线l对称.
(1)若圆心![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(2)点![]() 关于点
关于点![]() 的对称点为B,若圆
的对称点为B,若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)先求出圆心坐标,可得圆的方程,再设出切线方程,利用点到直线的距离公式,即可求得切线方程;
(2)设出点C,M的坐标,利用![]() ,寻找坐标之间的关系,进一步将问题转化为圆与圆的位置关系,即可得出结论.
,寻找坐标之间的关系,进一步将问题转化为圆与圆的位置关系,即可得出结论.
(1)由![]() 得圆心C为(1,-4),∵圆C的半径为1
得圆心C为(1,-4),∵圆C的半径为1
∴圆C的方程为: ![]()
显然切线的斜率一定存在,设所求圆C的切线方程为![]() ,即
,即![]() ∴
∴![]() ∴
∴![]()
![]()
∴所求圆C的切线方程为: ![]() 或者
或者![]()
(2)依题意求得B(-1,1)
∵圆C的圆心在在直线![]() 上,所以,设圆心C为(a,a-5)
上,所以,设圆心C为(a,a-5)
又∵![]()
∴设M为(x,y),则![]()
整理得: ![]() 设为圆D
设为圆D
∴点M应该既在圆C上又在圆D上,即圆C和圆D有交点
∴![]() ∴
∴![]()
由![]() 得
得![]()
由![]() 得
得![]()
终上所述,a的取值范围为: ![]()


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为![]() ,其范围为
,其范围为![]() ,分为五个级别,
,分为五个级别, ![]() 畅通;
畅通; ![]() 基本畅通;
基本畅通; ![]() 轻度拥堵;
轻度拥堵; ![]() 中度拥堵;
中度拥堵; ![]() 严重拥堵.早高峰时段(
严重拥堵.早高峰时段(![]() ),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.
),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.

(1)这50个路段为中度拥堵的有多少个?
(2)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟,中度拥堵为42分钟,严重拥堵为60分钟,求此人所用时间的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() 且与圆
且与圆![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 且斜率不为零的直线交曲线
且斜率不为零的直线交曲线![]() 于
于![]() ,
, ![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 的斜率之积为非零常数?若存在,求出定点的坐标;若不存在,请说明理由.
的斜率之积为非零常数?若存在,求出定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科)某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续驶里程数![]() (单位:公里)分为3类,即
(单位:公里)分为3类,即![]() ,
, ![]() ,
, ![]() .对这140辆车的行驶总里程进行统计,结果如下表:
.对这140辆车的行驶总里程进行统计,结果如下表:

(1)从这140辆汽车中任取1辆,求该车行驶总里程超过5万公里的概率; (2)公司为了了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车. (ⅰ)求
辆车. (ⅰ)求![]() 的值; (ⅱ)如果从这
的值; (ⅱ)如果从这![]() 辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率.
辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共l2分)
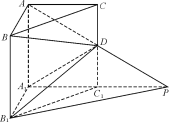
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com