
【题目】设![]() (e为自然对数的底数),
(e为自然对数的底数),![]() .
.
(I)记![]() .
.
(i)讨论函数![]() 单调性;
单调性;
(ii)证明当![]() 时,
时,![]() 恒成立
恒成立
(II)令![]() ,设函数G(x)有两个零点,求参数a的取值范围.
,设函数G(x)有两个零点,求参数a的取值范围.
【答案】(Ⅰ)(i)当![]() 时,
时, ![]() 单调减;当
单调减;当![]() 时,
时, ![]() 单调增;(ii)见解析;
单调增;(ii)见解析;
(Ⅱ)![]()
【解析】
试题(Ⅰ)(1)由函数![]() 求出它的导函数
求出它的导函数![]() ,根据其导函数的正负,即可得到函数单调区间即可.
,根据其导函数的正负,即可得到函数单调区间即可.
(2)构造函数![]() ,对
,对![]() 进行讨论,证明其最小值大于0.
进行讨论,证明其最小值大于0.
(Ⅱ)![]() ,
,![]() ,通过对
,通过对![]() 分类讨论研究其单调性,得到有两个零点时
分类讨论研究其单调性,得到有两个零点时![]() 的范围.
的范围.
试题解析:(Ⅰ)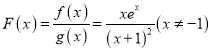 .
.
![]()
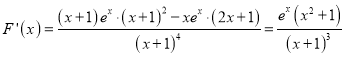 ,
,
所以,当![]() 时,
时,![]() ,
,![]() 单调减;
单调减;
当![]() 时,
时,![]() ,
,![]() 单调增.
单调增.
![]()
![]() ,
,
令![]() ,
,![]() ,
,
 ,
,
所以![]() ,又
,又![]() ,所以
,所以
![]() 时,
时,![]() 恒成立,即
恒成立,即
当![]() 时,
时,![]() 恒成立.
恒成立.
(Ⅱ)由已知,![]() ,
,
![]() .
.
当![]() 时,
时,![]() ,有唯一零点
,有唯一零点![]() ;
;
②当![]() 时,
时,![]() ,所以
,所以
当![]() 时,
时,![]() ,
,![]() 单调减;
单调减;
当![]() 时,
时,![]() ,
,![]() 单调增.
单调增.
所以![]() ,
,
因![]() ,所以当
,所以当![]() 时有唯一零点;
时有唯一零点;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以,![]() ,且
,且![]() ,当
,当![]() ,或
,或![]() 时,使
时,使![]() ,
,
取![]() ,则
,则![]() ,从而可知
,从而可知
当![]() 时,
时,![]() 有唯一零点,
有唯一零点,
即当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
③当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() ,或
,或![]() .
.
![]() 若
若![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 是单调减函数,至多有一个零点;
是单调减函数,至多有一个零点;
![]() 若
若![]() ,即
,即![]() 时,
时,![]() ,注意到
,注意到![]() ,
,![]() 都是增函数,所以
都是增函数,所以
当![]() 时,
时,![]() ,
,![]() 是单调减函数;
是单调减函数;
当![]() 时,
时,![]() ,
,![]() 是单调增函数;
是单调增函数;
当![]() 时,
时,![]() ,
,![]() 是单调减函数.
是单调减函数.
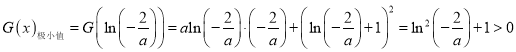 ,所以
,所以
![]() 至多有一个零点;
至多有一个零点;
![]() 若
若![]() ,即
,即![]() 时,同理可得
时,同理可得
当![]() 时,
时,![]() ,
,![]() 是单调减函数;
是单调减函数;
当![]() 时,
时,![]() ,
,![]() 是单调增函数;
是单调增函数;
当![]() 时,
时,![]() ,
,![]() 是单调减函数.
是单调减函数.
所以![]() ,
,![]() 至多有一个零点.
至多有一个零点.
综上,若函数![]() 有两个零点,则参数
有两个零点,则参数![]() 的取值范围是
的取值范围是![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】根据教育部高考改革指导意见,广东省从2021年正式实施“![]() ”新的高考考试方案.为尽快了解学生的选科需求,及时调整学校人力资源配备.某校从高一学生中抽样调查了100名同学,在模拟分科选择中,一半同学(其中男生38人)选择了物理,另一半(其中男生14人)选择了历史.请完成以下
”新的高考考试方案.为尽快了解学生的选科需求,及时调整学校人力资源配备.某校从高一学生中抽样调查了100名同学,在模拟分科选择中,一半同学(其中男生38人)选择了物理,另一半(其中男生14人)选择了历史.请完成以下![]() 列联表,并判断能否有99.9%的把握说选科与性别有关?
列联表,并判断能否有99.9%的把握说选科与性别有关?
参考公式: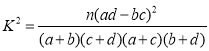 ,其中
,其中![]() 为样本容量.
为样本容量.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | |||
选物理 | 选历史 | 总计 | ||||||||
男生 | ||||||||||
女生 | ||||||||||
总计 | ||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4-4:坐标系与参数方程)
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是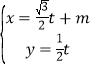 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且
,且![]() .
.
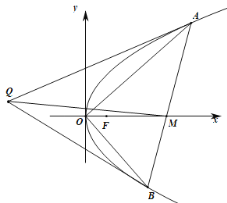
(1)求证:![]() ;
;
(2)求点![]() 的横坐标;
的横坐标;
(3)过![]() 点分别作抛物线的切线,两条切线交于点
点分别作抛物线的切线,两条切线交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
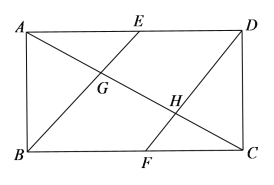
【题目】如图,一张矩形白纸![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,现分别将
的中点,现分别将![]() ,
,![]() 沿
沿![]() ,DF折起,且
,DF折起,且![]() 、
、![]() 在平面
在平面![]() 同侧,下列命题正确的是_________(写出所有正确命题的序号)
同侧,下列命题正确的是_________(写出所有正确命题的序号)
①平面![]() 平面
平面![]() 时,
时,![]()
②当平面![]() 平面
平面![]() 时,
时,![]() 平面
平面![]()
③当![]() 、
、![]() 重合于点
重合于点![]() 时,
时,![]()
④当![]() 、
、![]() 重合于点
重合于点![]() 时,三棱锥
时,三棱锥![]() 的外接球的半径为
的外接球的半径为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com