
【题目】已知二次函数f(x)=ax2+2x+c的对称轴为x=1,g(x)=x+ ![]() (x>0).
(x>0).
(1)求函数g(x)的最小值及取得最小值时x的值;
(2)试确定c的取值范围,使g(x)﹣f(x)=0至少有一个实根;
(3)若F(x)=﹣f(x)+4x+c,存在实数t,对任意x∈[1,m],使F(x+t)≤3x恒成立,求实数m的取值范围.
【答案】
(1)解:∵x>0,∴ ![]() ,
,
∴ ![]() ,当且仅当
,当且仅当 ![]() ,即x=1时“=”成立,即g(x)min=2,此时x=1
,即x=1时“=”成立,即g(x)min=2,此时x=1
(2)解:f(x)的对称轴为x=1,
∴a=﹣1,
∴f(x)=﹣x2+2x+c,g(x)﹣f(x)=0至少有一个实根,
∴g(x)=f(x)至少有一个实根,
即g(x)与f(x)的图象在(0,+∞)上至少有一个交点,f(x)=﹣(x﹣1)2+1+c,
∴f(x)max=1+c,g(x)min=2,
∴1+c≥2,∴c≥1,
∴c的取值范围为[1,+∞)
(3)解:F(x)=x2﹣2x﹣c+4x+c=x2+2x,
∴F(x+t)=(x+t)2+2(x+t),
由已知存在实数t,对任意x∈[1,m],使(x+t)2+2(x+t)≤3x恒成立.
∴x2+(2t﹣1)x+t2+2t≤0.
令h(x)=x2+(2t﹣1)x+t2+2t,
∴ ![]() ,即
,即 ![]() ,
,
转化为存在t∈[﹣4,0],使t2+(2m+2)t+m2﹣m≤0成立.
令G(t)=t2+(2m+2)t+m2﹣m,
∴G(t)的对称轴为t=﹣(m+1),
∵m>1,
∴﹣(m+1)<﹣2.
①当﹣4<﹣(m+1)<﹣2,即1<m<3时,
![]() ,
,
∴ ![]() ,
,
∴1<m<3.
②当﹣(m+1)≤﹣4,即m≥3时,
![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴3≤m≤8.
综上,实数m的取值范围为(1,8]
【解析】(1)根据基本不等式即可求出函数的最值;(2)根据对称轴求出a=﹣1,分别求出f(x)max=1+c,g(x)min=2,即1+c≥2,解得即;(3)把f(x+t)≤3x转化为(x+t)2+2(x+t)≤3x,即h(x)=x2+(2t﹣1)x+t2+2t,在x∈[1,m]恒小于0问题,考查h(x)的图象与性质,求出m的取值范围.


科目:高中数学 来源: 题型:
【题目】某人要利用无人机测量河流的宽度,如图,从无人机A处测得正前方河流的两岸B,C的俯角分别为75°,30°,此时无人机的高是60米,则河流的宽度BC等于( ) 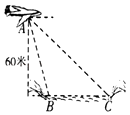
A.![]() 米
米
B.![]() 米
米
C.![]() 米
米
D.![]() 米
米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 为偶函数,且函数的y=f(x)图象相邻的两条对称轴间的距离为
为偶函数,且函数的y=f(x)图象相邻的两条对称轴间的距离为 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)将y=f(x)的图象向右平移 ![]() 个单位后,再将所得的图象上个点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在
个单位后,再将所得的图象上个点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在 ![]() 上的最值.
上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知射线OA:x﹣y=0(x≥0),OB:2x+y=0(x≥0).过点P(1,0)作直线分别交射线OA,OB于点A,B.
(1)当AB的中点在直线x﹣2y=0上时,求直线AB的方程;
(2)当△AOB的面积取最小值时,求直线AB的方程.
(3)当PAPB取最小值时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=r2(r>0),点P为圆O上任意一点(不在坐标轴上),过点P作倾斜角互补的两条直线分别交圆O于另一点A,B.
(1)当直线PA的斜率为2时,
①若点A的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),求点P的坐标;
),求点P的坐标;
②若点P的横坐标为2,且PA=2PB,求r的值;
(2)当点P在圆O上移动时,求证:直线OP与AB的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() 表示焦点在x轴上的椭圆,命题q:方程(k﹣1)x2+(k﹣3)y2=1表示双曲线.若p∨q为真,p∧q为假,求实数k的取值范围.
表示焦点在x轴上的椭圆,命题q:方程(k﹣1)x2+(k﹣3)y2=1表示双曲线.若p∨q为真,p∧q为假,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com