练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】《九章算术》中有一分鹿问题：“今有大夫、不更、簪袅、上造、公士，凡五人，共猎得五鹿.欲以爵次分之，问各得几何.”在这个问题中，大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员，现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组（一组2人，一组3人），派去两地执行公务，则大夫、不更恰好在同一组的概率为（ ）

    A.B.C.D.

    【答案】B

    【解析】

    基本事件总数，大夫、不更恰好在同一组包含的基本事件个数，由此能求出大夫、不更恰好在同一组的概率．

    皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人，一组3人)，派去两地执行公务， 基本事件总数，

    大夫、不更恰好在同一组包含的基本事件个数，

    所以大夫、不更恰好在同一组的概率为．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：，，为椭圆的左、右顶点，椭圆的右焦点为，椭圆的离心率为.

    （1）设直线与椭圆交于，两点，且，求的值；

    （2）设过点且斜率为1的直线与椭圆交于，（其中，分别在轴的上、下方）两点，当时，记、的面积分别为、，求的最小值，并求此时椭圆的标准方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线的参数方程为为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求直线的普通方程和曲线的直角坐标方程；

    （2）设点，直线与曲线交于两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线焦点为，直线过与抛物线交于两点.到准线的距离之和最小为8.

    （1）求抛物线方程；

    （2）若抛物线上一点纵坐标为，直线分别交准线于.求证：以为直径的圆过焦点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新高考方案规定，普通高中学业水平考试分为合格性考试（合格考）和选择性考试（选择考）.其中“选择考”成绩将计入高考总成绩，即“选择考”成绩根据学生考试时的原始卷面分数，由高到低进行排序，评定为A，B，C，D，E五个等级.某试点高中2019年参加“选择考”总人数是2017年参加“选择考”总人数的2倍，为了更好地分析该校学生“选择考”的水平情况，统计了该校2017年和2019年“选择考”成绩等级结果，得到如图表：

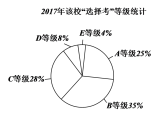
    针对该校“选择考”情况，2019年与2017年比较，下列说法正确的是( )

    A.获得A等级的人数不变B.获得B等级的人数增加了1倍

    C.获得C等级的人数减少了D.获得E等级的人数不变

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数（其中）的图象如图所示，为了得到的图象，则只要将的图象上所有的点（ ）

    A.向左平移个单位长度，纵坐标缩短到原来的，横坐标不变

    B.向左平移个单位长度，纵坐标伸长到原来的3倍横坐标不变

    C.向右平移个单位长度，纵坐标缩短到原来的，横坐标不变

    D.向右平移个单位长度，纵坐标伸长到原来的3倍，横坐标不变

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC-A1B1C1中，D,E分别是AB，BB1的中点.

    （Ⅰ）证明： BC1//平面A1CD;

    （Ⅱ）设AA1= AC=CB=2，AB=2，求三棱锥C一A1DE的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲乙两位同学玩游戏，对于给定的实数，按下列方法操作一次产生一个新的实数：由甲、乙同时各掷一枚均匀的硬币，如果出现两个正面朝上或两个反面朝上，则把乘以2后再减去6；如果出现一个正面朝上，一个反面朝上，则把除以2后再加上6，这样就可得到一个新的实数，对实数仍按上述方法进行一次操作，又得到一个新的实数，当时，甲获胜，否则乙获胜，若甲胜的概率为，则的取值范围是____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图在矩形ABCD中，AB＝5，AD＝2，点E在线段AB上，且BE＝1，将△ADE沿DE折起到A1DE的位置，使得平面A1DE⊥平面BCDE．

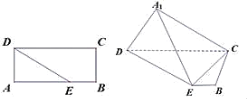
    （1）求证：CE⊥平面A1DE；

    （2）线段A1C上是否存在一点F，使得BF//平面A1DE？说明理由．

    查看答案和解析>>

    同步练习册答案