
(1)设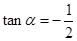 ,求
,求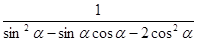 的值;
的值;
(2)已知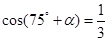 ,且
,且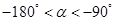 ,求
,求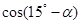 的值.
的值.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)将所求式分子1换成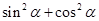 ,然后分子分母同除以
,然后分子分母同除以 ,将其转化为关于
,将其转化为关于 的式子再进行计算即可,本题若由
的式子再进行计算即可,本题若由 ,去求出
,去求出 ,则需要讨论,若想不到用
,则需要讨论,若想不到用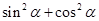 代替1,则可原式分子分母同除以
代替1,则可原式分子分母同除以 ,然后再考虑求出
,然后再考虑求出 ,显然这两种方法较为麻烦;(2)此类给三角函数值求三角函数值的问题一般是通过考察条件中的角和问题中的角的关系,然后通过诱导公式、同角三角函数关系式、和差角公式进行计算.注意到
,显然这两种方法较为麻烦;(2)此类给三角函数值求三角函数值的问题一般是通过考察条件中的角和问题中的角的关系,然后通过诱导公式、同角三角函数关系式、和差角公式进行计算.注意到 ,由诱导公式知
,由诱导公式知 ,结合条件由同角三角函数关系式可求出
,结合条件由同角三角函数关系式可求出 ,注意公式使用时要考察角的范围从而确定三角函数值的符号.
,注意公式使用时要考察角的范围从而确定三角函数值的符号.
试题解析:(1)原式= 3分
3分
 7分
7分
(2)由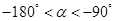 ,得
,得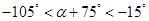 ,
,
故 10分
10分
而
所以 14分
14分
考点:同角三角函数的关系、三角函数的诱导公式.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com