
 .
.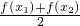 >f(
>f(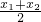 )成立;
)成立;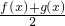 ,
, .
.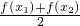 =
= -a(x1+x2)-aln(x1x2),
-a(x1+x2)-aln(x1x2),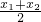 )=
)=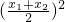 -a(x1+x2)-2aln
-a(x1+x2)-2aln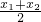
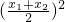 -a(x1+x2)-aln
-a(x1+x2)-aln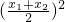
 -
-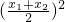 =
= >0(x1≠x2),∴
>0(x1≠x2),∴ >
>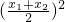 ①
①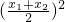 ∴lnx1x2<ln
∴lnx1x2<ln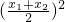
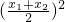 ②
②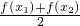 >f(
>f(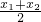 ).
).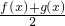 =
= x2-ax-alnx+
x2-ax-alnx+ ln2x+a2+
ln2x+a2+ .
.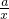 +
+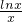
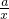 +
+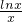 ,则y=F(x)在[1,+∞)上单调递增.
,则y=F(x)在[1,+∞)上单调递增. ,则当x≥1时,x2-lnx+a+1≥0恒成立.
,则当x≥1时,x2-lnx+a+1≥0恒成立. <0.
<0. x2-ax-alnx+
x2-ax-alnx+ ln2x+a2+
ln2x+a2+ =a2-(x+lnx)a+
=a2-(x+lnx)a+ (x2+ln2x)+
(x2+ln2x)+ .
. (x2+ln2x),则P(a)=(a-
(x2+ln2x),则P(a)=(a- )2+
)2+ ≥
≥ .
. =
= .
. .
. +
+ =
= .
.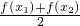 与f(
与f(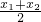 );然后通过作差法或基本不等式等知识比较两代数式中部分的大小;最后得出两代数式整体的大小.
);然后通过作差法或基本不等式等知识比较两代数式中部分的大小;最后得出两代数式整体的大小. (x2+ln2x)+
(x2+ln2x)+ ;然后利用配方法得P(a)=a2-(x+lnx)a+
;然后利用配方法得P(a)=a2-(x+lnx)a+ (x2+ln2x)=(a-
(x2+ln2x)=(a- )2+
)2+ ≥
≥ ;再通过构造函数Q(x)=x-lnx,并由导数法求其最小值进而得P(a)的最小值;最后得h(x)的最小值,即问题得证.
;再通过构造函数Q(x)=x-lnx,并由导数法求其最小值进而得P(a)的最小值;最后得h(x)的最小值,即问题得证.

 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| f( x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x)+g(x) |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省十二校高三第二次联考数学试卷(理科)(解析版) 题型:解答题
 .
. >f(
>f( )成立;
)成立; ,
, .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省张家界市高三联考数学试卷1(理科)(解析版) 题型:解答题
 )+
)+
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com