
【题目】已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)=2g(x)+ ![]() ,若f(
,若f( ![]() )+f(cos2θ)<f(π)﹣f(
)+f(cos2θ)<f(π)﹣f( ![]() ),则θ的取值范围是( )
),则θ的取值范围是( )
A.(2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ),k∈Z
),k∈Z
B.(2kπ﹣ ![]() ,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+
,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+ ![]() π),k∈Z
π),k∈Z
C.(2kπ﹣ ![]() ,2kπ﹣
,2kπ﹣ ![]() ),k∈Z
),k∈Z
D.(2kπ﹣ ![]() ,2kπ﹣π)∪(2kπ﹣π,2kπ)∪(2kπ,2kπ+
,2kπ﹣π)∪(2kπ﹣π,2kπ)∪(2kπ,2kπ+ ![]() ),k∈Z
),k∈Z
【答案】C
【解析】解:由题意,﹣f(x)=2g(x)+ ![]() ,f(x)=2g(x)+
,f(x)=2g(x)+ ![]() , ∴f(x)=
, ∴f(x)= ![]() ,∴f(
,∴f( ![]() )=
)= ![]() ,
,
又f′(x)= ![]() ,∴函数f(x)在(﹣1,1)上单调递增,(﹣∞,﹣1),(1,+∞)上单调递减
,∴函数f(x)在(﹣1,1)上单调递增,(﹣∞,﹣1),(1,+∞)上单调递减
∵f( ![]() )+f(cos2θ)<f(π)﹣f(
)+f(cos2θ)<f(π)﹣f( ![]() ),
),
∴f( ![]() )+f(cos2θ)<0,
)+f(cos2θ)<0,
∴f(sinθ)<f(﹣cos2θ),且sinθ≠0
∴sinθ<﹣cos2θ,且sinθ≠0
∴2sin2θ﹣sinθ﹣1>0,且sinθ≠0
∴sinθ<﹣ ![]() ,且sinθ≠0,
,且sinθ≠0,
∴θ∈(2kπ﹣ ![]() ,2kπ﹣
,2kπ﹣ ![]() ),k∈Z,
),k∈Z,
故选C.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)的导函数为f'(x),满足x2f'(x)+xf(x)=lnx,f(e)= ![]() ,则f(x)( )
,则f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 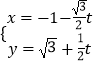 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 ![]() .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设点为P(x,y)为直线l与圆C所截得的弦上的动点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() +
+ ![]() =1(a>b>0)的离心率与双曲线x2﹣y2=a2的离心率之和为
=1(a>b>0)的离心率与双曲线x2﹣y2=a2的离心率之和为 ![]() ,B1、B2为椭圆Γ短轴的两个端点,P是椭圆Γ上一动点(不与B1、B2重合),直线B1P、B2P分别交直线l:y=4于M、N两点,△B1B2P的面积记为S1 , △PMN的面积记为S2 , 且S1的最大值为4
,B1、B2为椭圆Γ短轴的两个端点,P是椭圆Γ上一动点(不与B1、B2重合),直线B1P、B2P分别交直线l:y=4于M、N两点,△B1B2P的面积记为S1 , △PMN的面积记为S2 , 且S1的最大值为4 ![]() .
.
(1)求椭圆Γ的方程;
(2)若S2=λS1 , 当λ取最小值时,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an},a1=﹣ll,公差d≠0,且a2 , a5 , a6成等比数列.
(1)求数列{an}的通项公式;
(2)若bn=|an|,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年高考中,某省10万考生在满分为150分的数学考试中,成绩分布近似服从正态分布N(110,100),则分数位于区间(130,150]分的考生人数近似为( ) (已知若X~N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544,P(μ﹣3σ<X<μ+3σ)=0.9974.
A.1140
B.1075
C.2280
D.2150
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com