【题目】某兴趣小组有男生20人，女生10人，从中抽取一个容量为5的样本，恰好抽到2名男生和3名女生，则
①该抽样可能是系统抽样；
②该抽样可能是随机抽样：
③该抽样一定不是分层抽样；
④本次抽样中每个人被抽到的概率都是
．
其中说法正确的为（ ）
A.①②③B.②③C.②③④D.③④
【答案】A
【解析】
①该抽样可以是系统抽样；②因为总体个数不多，容易对每个个体进行编号，因此该抽样可能是简单的随机抽样；③若总体由差异明显的几部分组成时，经常采用分层抽样的方法进行抽样，且分层抽样的比例相同，该抽样不可能是分层抽样；④分别求出男生和女生的概率，故可判断出真假.
①总体容量为30，样本容量为5，第一步对30个个体进行编号，如男生1～20，女生21～30；
第二步确定分段间隔
；第三步在第一段用简单随机抽样确定第一个个体编号
；
第四步将编号为
依次抽取，即可获得整个样本．故该抽样可以是系统抽样．因此①正确．
②因为总体个数不多，可以对每个个体进行编号，因此该抽样可能是简单的随机抽样，故②正确；
③若总体由差异明显的几部分组成时，经常采用分层抽样的方法进行抽样，且分层抽样的比例相同，
但兴趣小组有男生20人，女生10人，抽取2男3女，抽的比例不同，故③正确；
④该抽样男生被抽到的概率
；女生被抽到的概率
，故前者小于后者．因此④不正确．
故选：A．
科目：高中数学 来源： 题型：
【题目】已知圆C：
.
(1)若直线
在y轴上的截距为0且不与x轴重合，与圆C交于
，试求直线
:
在x轴上的截距;
（2）若斜率为1的直线
与圆C交于D,E两点，求使
面积的最大值及此时直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市甲、乙两地为了争创“市级文明城市”，现市文明委对甲、乙两地各派10名专家进行打分评优，所得分数情况如下茎叶图所示.
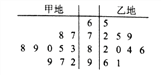
（1）分别计算甲、乙两地所得分数的平均值，并计算乙地得分的中位数；
（2）从乙地所得分数在
间的成绩中随机抽取2份做进一步分析，求所抽取的成绩中，至少有一份分数在
间的概率；
（3）在甲、乙两地所得分数超过90分的成绩中抽取其中2份分析其合理性，求这2份成绩都是来自甲地的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数
被称为狄利克雷函数，其中
为实数集，
为有理数集，则关于函数
有如下四个命题：①
；②函数是偶函数；③任取一个不为零的有理数
，
对任意的
恒成立；④存在三个点
，
，
，使得
为等边三角形.其中真命题的个数有（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》中盈不足章中有这样一则故事：“今有良马与驽马发长安，至齐. 齐去长安三千里. 良马初日行一百九十三里，日增一十二里；驽马初日行九十七里，日减二里．” 为了计算每天良马和驽马所走的路程之和，设计框图如下图. 若输出的 
的值为 360，则判断框中可以填( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
且
，函数
在点
处的切线过点 
.
(1) 求
满足的关系式，并讨论函数
的单调区间；
(2)已知
，若函数
在
上有且只有一个零点，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的图像经过点
，且
的相邻两个零点的距离为
，为得到
的图像，可将
图像上所有点（ ）
A.先向右平移
个单位，再将所得图像上所有点的横坐标缩短为原来的
，纵坐标不变
B.先向左平移个单位，再将所得图像上所有点的横坐标缩短为原来的，纵坐标不变
C.先向左平移个单位，再将所得图像上所有点的横坐标伸长为原来的2倍，纵坐标不变
D.先向右平移个单位，再将所得图像上所有点的横坐标伸长为原来的2倍，纵坐标不变
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】曙光中学团委组织了“弘扬奥运精神，爱我中华”的知识竞赛，从参加考试的学生中抽出
名学生，将其成绩(均为整数)分成六段
，
，
，
后画出如下部分频率分布直方图，则第四小组的频率为_______，从成绩是和的学生中选两人，他们在同一分数段的概率_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
