
分析 (1)利用直角坐标化为极坐标的公式,即可得出结论;
(2)利用S△PQR=S△POR+S△OQR-S△POQ,即可求△PQR的面积.
解答 解 (1)P(2$\sqrt{3}$,2),极径4,极角$\frac{π}{6}$,Q(4,-4),极径4$\sqrt{2}$,极角-$\frac{π}{4}$,R(6,0),极径6,极角0.
∴P(4,$\frac{π}{6}$),Q(4$\sqrt{2}$,-$\frac{π}{4}$),R(6,0). (6分) (每个2分)
(2)S△PQR=S△POR+S△OQR-S△POQ
=$\frac{1}{2}$×4×6×sin $\frac{π}{6}$+$\frac{1}{2}$×4$\sqrt{2}$×6×sin $\frac{π}{4}$-$\frac{1}{2}$×4×4$\sqrt{2}$sin$\frac{5π}{12}$
=14-4$\sqrt{3}$.(12分)
点评 本题考查直角坐标化为极坐标,考查三角形面积计算,比较基础.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE.
如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知AB,DE为圆O的直径,CD⊥AB于N,N为OB的中点,EB与CD相交于点M,切线EF与DC的延长线交于点F.若圆O的半径为1,则EF的长为( )
已知AB,DE为圆O的直径,CD⊥AB于N,N为OB的中点,EB与CD相交于点M,切线EF与DC的延长线交于点F.若圆O的半径为1,则EF的长为( )| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{21}}}{3}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
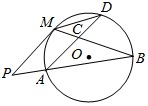 如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则CD等于( )
如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则CD等于( )| A. | $\frac{16}{9}$ | B. | $\frac{4}{3}$ | C. | $\frac{9}{16}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图是某学院抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为20,则抽取的学生人数为80.
如图是某学院抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为20,则抽取的学生人数为80.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com