
【题目】设函数f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
【答案】(1)a=4,b=2; (2)当x=2时,函数f(x)取最大值lg12,(3)![]()
【解析】试题分析:(1)根据条件得到关于a,b的方程组求解可得a=4,b=2;(2)由(1)得:函数f(x)=lg(4x﹣2x),根据x∈[1,2],可得![]() ,再由函数的单调性求最值;(3)设t=2x,将问题转化成方程
,再由函数的单调性求最值;(3)设t=2x,将问题转化成方程![]() 有两个正解处理,根据判别式和根与系数的关系可求解。
有两个正解处理,根据判别式和根与系数的关系可求解。
试题解析:(1)∵f(1)=lg2,f(2)=lg12, f(x)=lg(ax﹣bx)
∴![]() ,解得
,解得![]() 。
。
∴a=4,b=2;
(2)由(1)得:函数f(x)=lg(4x﹣2x),
当![]() 时,
时, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
故当![]() ,即x=2时,函数f(x)取最大值lg12。
,即x=2时,函数f(x)取最大值lg12。
(3)若函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
则方程4x﹣2x=m有两个解,
令t=2x,则t>0,
则方程![]() 有两个正解;
有两个正解;
故![]() , 解得
, 解得![]() 。
。
所以当![]() 时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点。
时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点。


科目:高中数学 来源: 题型:
【题目】如图甲,直角梯形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 与平面
与平面![]() 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
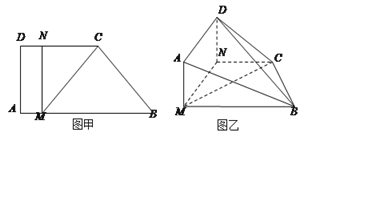
(II)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
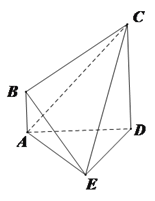
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求![]() 的值;
的值;

(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来篷勃发展的新机遇,2016年双11期间,某购物平台的销售业绩高达一千多亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(Ⅰ)请完成如下列联表;
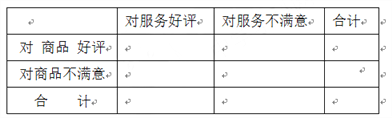
(Ⅱ)是否可以在犯错误的概率不超过0.1%的前提下,认为商品好评与服务好评有关?
(Ⅲ)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.

( ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com