练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知锐角△ABC的三个内角A，B，C的对边分别为a，b，c，且 =（a，b+c）， ．
    （1）求角A；
    （2）若a=3，求△ABC面积的取值范围．

    【答案】
    （1）解：由 ，得

    由正弦定理得

    因为B=π﹣A﹣C

    所以

    所以

    由于sinC≠0，所以

    由 ，得 ，故 .


    （2）解：由 ，得 ，

    所以 =

    由△ABC为锐角三角形，所以 ，得 ，

    所以 ， ，

    故6＜bc≤9，

    又 ，

    所以，△ABC面积的取值范围为 ．


    【解析】（1）由 ，结合正弦定理，通过B=π﹣A﹣C，化简表达式利用两角和与差的三角函数推出 锐角求解A．（2）利用正弦定理以及两角和与差的三角函数，结合B的范围，求解三角形的面积的范围即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1、AD的中点，那么异面直线OE和FD1所成的角的余弦值等于（ ）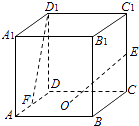

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，点P是平面A1BC1内一动点，且满足|PD|+|PB1|=6，则点P的轨迹所形成的图形的面积是（ ）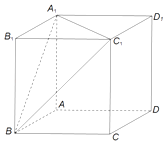
    A.2π
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：（x﹣3）2+（y﹣4）2=4
    （1）若平面上有两点A（1，0），B（﹣1，0），点P是圆C上的动点，求使|AP|2+|BP|2取得最小值时点P的坐标；
    （2）若Q是x轴上的动点，QM，QN分别切圆C于M，N两点，①若 ，求直线QC的方程；②求证：直线MN恒过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某科研小组研究发现：一棵水果树的产量（单位：百千克）与肥料费用（单位：百元）满足如下关系： .此外，还需要投入其它成本（如施肥的人工费等）百元.已知这种水果的市场售价为16元/千克（即16百元/百千克），且市场需求始终供不应求.记该棵水果树获得的利润为（单位：百元）.

    （1）求的函数关系式；

    当投入的肥料费用为多少时，该水果树获得的利润最大？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 ．
    （1）若 与 垂直，求k的值；
    （2）若 与 平行，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点P（t，t），点M是圆O1：x2+（y﹣1）2= 上的动点，点N是圆O2：（x﹣2）2+y2= 上的动点，则|PN|﹣|PM|的最大值是（ ）
    A.1
    B. ﹣2
    C.2+
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f （ x）=ax3+bx2+cx+d 的图象如图所示，则 的取值范围是（ ）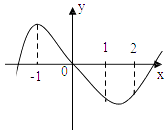
    A.（﹣ ， ?）
    B.（﹣ ，1）
    C.（﹣ ， ）
    D.（﹣ ，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】按下列程序框图运算，则输出的结果是（ ）
    A.42
    B.128
    C.170
    D.682

    查看答案和解析>>

    同步练习册答案