
【题目】已知过点![]() 的动直线
的动直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 两点.当直线
两点.当直线![]() 的斜率是
的斜率是![]() 时,
时,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设线段![]() 的中垂线在
的中垂线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)x2=4y;(2)b∈(2,+∞).
【解析】
试题分析:本题主要考查抛物线的标准方程、直线与抛物线的交点问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用点斜式先写出直线![]() 的方程,令直线与抛物线联立,消参得到关于y的方程,利用韦达定理,得到
的方程,令直线与抛物线联立,消参得到关于y的方程,利用韦达定理,得到![]() 和
和![]() ,再利用
,再利用![]() ,解出
,解出![]() ,得到抛物线的方程;第二问,设出直线
,得到抛物线的方程;第二问,设出直线![]() 的方程,令抛物线与直线联立,消参得到关于x的方程,利用韦达定理,得到BC的中点坐标,从而得到BC的中垂线方程,令x=0,得到中垂线在y轴上的截距,再通过配方法求范围.
的方程,令抛物线与直线联立,消参得到关于x的方程,利用韦达定理,得到BC的中点坐标,从而得到BC的中垂线方程,令x=0,得到中垂线在y轴上的截距,再通过配方法求范围.
试题解析:(1)设B(x1,y1),C(x2,y2),当直线l的斜率是时,l的方程为y=(x+4),即x=2y-4.
由 得2y2-(8+p)y+8=0,
得2y2-(8+p)y+8=0,
∴![]() ①,
①, ![]() ②
②
又∵![]() ,∴y2=4y1,③
,∴y2=4y1,③
由①②③及p>0得:y1=1,y2=4,p=2,得抛物线G的方程为x2=4y.
(2)设l:y=k(x+4),BC的中点坐标为(x0,y0),
由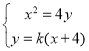 得x2-4kx-16k=0,④
得x2-4kx-16k=0,④
∴![]() ,y0=k(x0+4)=2k2+4k.
,y0=k(x0+4)=2k2+4k.
∴线段BC的中垂线方程为y-2k2-4k=-![]() (x-2k),
(x-2k),
∴线段BC的中垂线在y轴上的截距为:b=2k2+4k+2=2(k+1)2,
对于方程④,由Δ=16k2+64k>0得k>0或k<-4. ∴b∈(2,+∞).


科目:高中数学 来源: 题型:
【题目】某金匠以黄金为原材料加工一种饰品,经多年的数据统计得知,该金匠平均每加5 个饰品中有4个成品和1个废品,每个成品可获利3万元,每个废品损失1万元,假设该金匠加工每件饰品互不影响,以频率估计概率.
(1)若金金匠加工4个饰品,求其中废品的数量不超过1的概率;
(2)若该金匠加工了 3个饰品,求他所获利润的数学期望.
(两小问的计算结果都用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三上学期期末数学考试成绩中,随机抽取了![]() 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图:
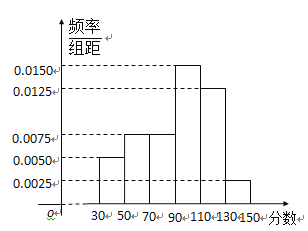
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,该
人,该![]() 人中成绩在
人中成绩在![]() 的有几人?
的有几人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求分数在
人,求分数在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点.
上的点.
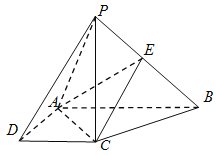
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙丙丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为 ![]() , 有以下结论:
, 有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当0<x<1时,丁在最前面,当x>1时,丁在最后面;
④丙不可能在最前面,也不可能最最后面;
⑤如果它们已知运动下去,最终在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com