
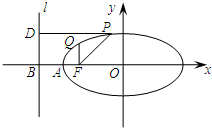
 如下图,椭圆中心为O,F是焦点,A为顶点,准线l交OA延长线于B,P,Q在椭圆上且PD⊥l于D,QF⊥OA于F,则以下比值①
如下图,椭圆中心为O,F是焦点,A为顶点,准线l交OA延长线于B,P,Q在椭圆上且PD⊥l于D,QF⊥OA于F,则以下比值①| |PF| |
| |PD| |
| |QF| |
| |BF| |
| |AO| |
| |BO| |
| |AF| |
| |BA| |
| |FO| |
| |AO| |
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
| |PF| |
| |PD| |
| a2 |
| c |
| b2 |
| c |
| b2 |
| a |
| |QF| |
| |BF| |
| c |
| a |
| a2 |
| c |
| |AO| |
| |BO| |
| c |
| a |
| |AF| |
| |BA| |
| |FO| |
| |AO| |
| c |
| a |


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:

①![]() ②
②![]() ③
③![]() ④
④![]() ⑤
⑤![]()
A.1个 B.2个 C.4个 D.5个
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
有一幅椭圆型彗星轨道图,长4cm,高![]() ,如下图,
,如下图,
已知O为椭圆中心,A1,A2是长轴两端点,
|
(Ⅰ)建立适当的坐标系,写出椭圆方程,
并求出当彗星运行到太阳正上方时二者在图上的距离;
(Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,
设P是l上异于D点的任意一点,直线A1P,A2P分别
交椭圆于M、N(不同于A1,A2)两点,问点A2能否
在以MN为直径的圆上?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
如下图,已知△OFQ的面积为S,且![]() ·
·![]() =1,
=1,
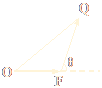
(1)若S的范围为![]() <S<2,求向量
<S<2,求向量![]() 与
与![]() 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设|![]() |=c(c≥2),S=
|=c(c≥2),S=![]() c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|![]() |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省武汉市华中师大一附中高二(上)期中数学试卷(理科)(解析版) 题型:填空题
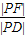 ②
② ③
③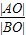 ④
④ ⑤
⑤ 能作为椭圆的离心率的是 (填写所有正确的序号)
能作为椭圆的离心率的是 (填写所有正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com