
【题目】在平面直角坐标系![]() 中,已知定点
中,已知定点![]() ,点
,点![]() 在
在![]() 轴上运动,点
轴上运动,点![]() 在
在![]() 轴上运动,点
轴上运动,点![]() 为坐标平面内的动点,且满足
为坐标平面内的动点,且满足![]() ,
,![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过曲线![]() 第一象限上一点
第一象限上一点![]() (其中
(其中![]() )作切线交直线
)作切线交直线![]() 于点
于点![]() ,连结
,连结![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,求当
,求当![]() 面积取最小值时切点
面积取最小值时切点![]() 的横坐标.
的横坐标.
科目:高中数学 来源: 题型:
【题目】如图1,平面五边形![]() 是由边长为2的正方形
是由边长为2的正方形![]() 与上底为1,高为
与上底为1,高为![]() 直角梯形
直角梯形![]() 组合而成,将五边形
组合而成,将五边形![]() 沿着
沿着![]() 折叠,得到图2所示的空间几何体,其中
折叠,得到图2所示的空间几何体,其中![]() .
.
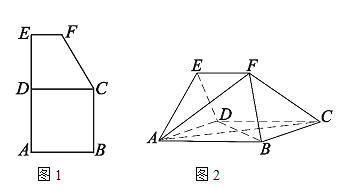
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是中国古代的著名数学著作,该书表明:至迟于公元5世纪,中国已经系统掌握等差数列的相关理论,该书上卷22题又“女工善织问题”:“今有女善织,日益功疾,初日织五尺,今一月曰织九匹三丈,问日益几何?”,大概意思是:有一个女工人善于织布,每天织布的尺数越来越多且成等差数列,第一天知5尺,30天共织九匹三丈,问每天增加的织布数目是多少寸?答案是__________寸.(注:当时一匹为四丈,一丈为十尺,一尺为十寸,结果四舍五入精确到寸)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为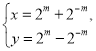 (m为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(m为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ρcosθ
ρcosθ![]() ρsinθ
ρsinθ![]() 2
2![]() =0.
=0.
(1)求C和l的直角坐标方程;
(2)设直线l与曲线C的公共点为P,Q,求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】坐标系与参数方程:在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上
上
(Ⅰ)求![]() 的值和直线
的值和直线![]() 的直角坐标方程及
的直角坐标方程及![]() 的参数方程;
的参数方程;
(Ⅱ)已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),直线
为参数),直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的所有棱长都为
的所有棱长都为![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 在
在![]() 边上,
边上,![]() .
.
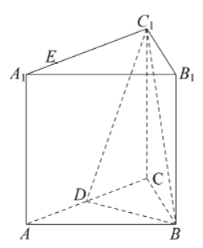
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是侧面
是侧面![]() 内的动点,且
内的动点,且![]() 平面
平面![]() .
.
①在答题卡中作出点![]() 的轨迹,并说明轨迹的形状(不需要说明理由);
的轨迹,并说明轨迹的形状(不需要说明理由);
②求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .把
.把![]() 沿着
沿着![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,连结
,连结![]() ,如图2.
,如图2.
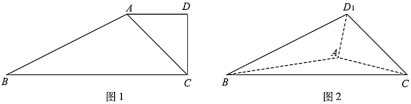
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com