
【题目】如图,一智能扫地机器人在![]() 处发现位于它正西方向的
处发现位于它正西方向的![]() 处和北偏东30°方向上的
处和北偏东30°方向上的![]() 处分别有需要清扫的垃圾,红外线感应测量发现机器人到
处分别有需要清扫的垃圾,红外线感应测量发现机器人到![]() 的距离比到
的距离比到![]() 的距离少0.4米,于是选择沿
的距离少0.4米,于是选择沿![]() 路线清扫,已知智能扫地机器人的直线行走速度为0.2
路线清扫,已知智能扫地机器人的直线行走速度为0.2![]() ,忽略机器人吸入垃圾及在
,忽略机器人吸入垃圾及在![]() 处旋转所用时间,10秒钟完成了清扫任务.
处旋转所用时间,10秒钟完成了清扫任务.
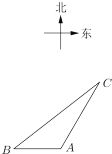
(1)![]() 、
、![]() 两处垃圾的距离是多少?
两处垃圾的距离是多少?
(2)智能扫地机器人此次清扫行走路线的夹角![]() 的正弦值是多少?
的正弦值是多少?
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖促销活动,规定每位顾客从装有编号为0,1,2,3四个相同小球的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码之和等于6,则中一等奖,等于5中二等奖,等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
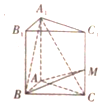
【题目】直三棱柱![]() 中,底面ABC为等腰直角三角形,
中,底面ABC为等腰直角三角形,![]() ,
,![]() ,
,![]() ,M是侧棱
,M是侧棱![]() 上一点,设
上一点,设![]() ,用空间向量知识解答下列问题.
,用空间向量知识解答下列问题.
![]() 1
1![]() 若
若![]() ,证明:
,证明:![]() ;
;
![]() 2
2![]() 若
若![]() ,求直线
,求直线![]() 与平面ABM所成的角的正弦值.
与平面ABM所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 恰有3个零点,则实数
恰有3个零点,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】![]() ,在
,在![]() 上单调递减.若
上单调递减.若![]() ,则
,则![]() 在
在![]() 上递增,那么零点个数至多有一个,不符合题意,故
上递增,那么零点个数至多有一个,不符合题意,故![]() .故需
.故需![]() 当
当![]() 时
时![]() ,且
,且![]() ,使得第一段有一个零点,故
,使得第一段有一个零点,故![]() .对于第二段,
.对于第二段, ![]() ,故需
,故需![]() 在区间
在区间![]() 有两个零点,
有两个零点, ![]() ,故
,故![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,所以
上递减,所以 ,解得
,解得![]() .综上所述,
.综上所述, ![]()
【点睛】本小题主要考查函数的图象与性质,考查含有参数的分段函数零点问题的求解策略,考查了利用导数研究函数的单调区间,极值,最值等基本问题.其中用到了多种方法,首先对于第一段函数的分析利用了分离常数法,且直接看出函数的单调性.第二段函数利用的是导数来研究图像与性质.
【题型】单选题
【结束】
13
【题目】设![]() ,
, ![]() 满足约束条件
满足约束条件 ,则
,则![]() 的最大值为_______.
的最大值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件,其长度误差落在区间(3,6)内的概率为( )
(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.27%,P(μ-2σ<ξ<μ+2σ)=95.45%.)
A. 4.56%B. 13.59%C. 27.18%D. 31.74%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com