
分析 (Ⅰ)利用对数性质、运算法则求解.
(Ⅱ)利用运用有理数指数幂数性质、运算法则求解
解答 解:(Ⅰ)$|{1+lg0.001}|+\sqrt{{{lg}^2}\frac{1}{3}-4lg3+4}+lg6-lg0.02$
=|1-3|+|lg3-2|+lg300
=2+2-lg3+lg3+2=6.…(8分)
(Ⅱ)${(-\frac{27}{8})^{-\frac{2}{3}}}+{0.002^{-\frac{1}{2}}}-10{(\sqrt{5}-2)^{-1}}+{(2-\sqrt{3})^0}$
=$\frac{4}{9}+10\sqrt{5}-10\sqrt{5}-20+1$
=-$\frac{167}{9}$. …(15分)
点评 本题考查对数式、指数式的化简求值,是基础题,解题时要认真审题,注意对数性质、运算法则和指数的性质、运算法则的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有 缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
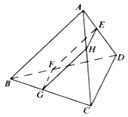 如图,在四面体ABCD中,AB=CD=2,AB与CD所成的角为45°,点E,F,G,H分别在棱EC,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是1.
如图,在四面体ABCD中,AB=CD=2,AB与CD所成的角为45°,点E,F,G,H分别在棱EC,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com