
【题目】将函数f(x)=2cos2x的图象向右平移 ![]() 个单位后得到函数g(x)的图象,若函数g(x)在区间[0,
个单位后得到函数g(x)的图象,若函数g(x)在区间[0, ![]() ]和[2a,
]和[2a, ![]() ]上均单调递增,则实数a的取值范围是( )
]上均单调递增,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
【答案】A
【解析】解:将函数f(x)=2cos2x的图象向右平移 ![]() 个单位后得到函数g(x)的图象, 得g(x)=2cos2(x﹣
个单位后得到函数g(x)的图象, 得g(x)=2cos2(x﹣ ![]() )=2cos(2x﹣
)=2cos(2x﹣ ![]() ),
),
由 ![]() ,得
,得 ![]() .
.
当k=0时,函数的增区间为[ ![]() ],当k=1时,函数的增区间为[
],当k=1时,函数的增区间为[ ![]() ].
].
要使函数g(x)在区间[0, ![]() ]和[2a,
]和[2a, ![]() ]上均单调递增,
]上均单调递增,
则 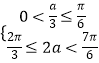 ,解得a∈[
,解得a∈[ ![]() ,
, ![]() ].
].
故选:A.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】下列命题:①集合![]() 的子集个数有
的子集个数有![]() 个;②定义在
个;②定义在![]() 上的奇函数
上的奇函数![]() 必满足
必满足![]() ;③
;③![]() 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与![]() 轴相交;⑤
轴相交;⑤![]() 在
在![]() 上是减函数,其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
上是减函数,其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,这是2017年我国重要的主场外交活动,对推动国际和地区合作具有重要意义.某高中政教处为了调查学生对“一带一路”的关注情况,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,得到其测试成绩(百分制),如茎叶图所示.
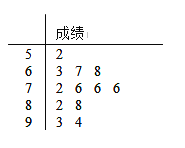
(1)写出该样本的众数、中位数,若该校共有3000名学生,试估计该校测试成绩在70分以上的人数;
(2)从所抽取的70分以上的学生中再随机选取4人.
①记![]() 表示选取4人的成绩的平均数,求
表示选取4人的成绩的平均数,求![]() ;
;
②记![]() 表示测试成绩在80分以上的人数,求
表示测试成绩在80分以上的人数,求![]() 的分布和数学期望.
的分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①已知X服从正态分布N(0,σ2),且P(﹣2≤X≤2)=0.6,则P(X>2)=0.2;
②若命题 ![]() ,则¬p:x∈(﹣∞,1),x2﹣x﹣1≥0;
,则¬p:x∈(﹣∞,1),x2﹣x﹣1≥0;
③已知直线l1:ax+3y﹣1=0,l2:x+by+1=0,则l1⊥l2的充要条件是 ![]() .
.
其中正确的结论的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品要了解年广告费![]() (单位:万元)对年利润
(单位:万元)对年利润![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年利润
和年利润![]() 数据作了初步整理,得到下面的表格:
数据作了初步整理,得到下面的表格:
广告费 | 2 | 3 | 4 | 5 |
年利润 | 26 | 39 | 49 | 54 |
(Ⅰ)用广告费作解释变量,年利润作预报变量,建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)根据(Ⅰ)的结果预报广告费用为6万元时的年利润.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列三角形数表: 
假设第n行的第二个数为 ![]() ,
,
(1)归纳出an+1与an的关系式,并求出an的通项公式;
(2)设anbn=1(n≥2),求证:b2+b3+…+bn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省农科站要检测某品牌种子的发芽率,计划采用随机数表法从该品牌![]() 粒种子中抽取
粒种子中抽取![]() 粒进行检测,现将这
粒进行检测,现将这![]() 粒种子编号如下
粒种子编号如下![]() ,
,![]() ,
,![]() ,
,![]() ,若从随机数表第
,若从随机数表第![]() 行第
行第![]() 列的数
列的数![]() 开始向右读,则所抽取的第
开始向右读,则所抽取的第![]() 粒种子的编号是 .(下表是随机数表第
粒种子的编号是 .(下表是随机数表第![]() 行至第
行至第![]() 行)
行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有________(只填序号)
①若直线与平面有无数个公共点,则直线在平面内;
②若直线l上有无数个点不在平面α内,则l∥α;
③若两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交;
④若直线l与平面α平行,则l与平面α内的直线平行或异面;
⑤若平面α∥平面β,直线aα,直线bβ,则直线a∥b.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com