
分析 (Ⅰ)由已知条件求得n的值,利用二项展开式的通项公式,可得展开式中所有有理项和二项式系数最大的项.
(Ⅱ)对于${(3x-1)^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$,分别给x赋值,可得要求式子的值.
解答 解:(Ⅰ)∵二项式${(\sqrt{x}+\frac{2}{{\root{3}{x}}})^n}({n∈{N^*}})$的前三项的系数的和为129,
∴${C}_{n}^{0}$+${C}_{n}^{1}$•2+${C}_{n}^{2}$•22=129,求得n=8,故展开式的通项公式为Tr+1=${C}_{8}^{r}$•2r•${x}^{4-\frac{5r}{6}}$,
令4-$\frac{5r}{6}$为整数,可得r=0,6,故此展开式中所有有理项为:T1=x4,T7=${C}_{8}^{6}$•x-1.
二项式系数最大的项为T5=${C}_{8}^{4}$•${x}^{\frac{2}{3}}$.
(Ⅱ)∵已知${(3x-1)^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$,
(1)在已知${(3x-1)^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$中,令x=0,可得a0=-1.
(2)在已知${(3x-1)^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$中,
令x=1可得a0+a1+a2+a3+…+a7 =27=128 ①,∴a1+a2+a3+…+a7 =27+1=129.
(3)在已知${(3x-1)^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$中,令x=-1,可得a0-a1+a2-a3+…-a7 =-47 ②,
把①式减去②式,并除以2,可得 a1+a3+a5+a7 =$\frac{128{+4}^{7}}{2}$.
(4)把①式加上②式,并除以2,可得a0+a2+a4+a6=$\frac{128{-4}^{7}}{2}$.
(5)根据${(3x-1)^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$,可得|a0|+|a1|+|a2|+…+|a7|即为(3x+1)7的展开式中各项系数和,为47.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | mn=1 | B. | mn=-1 | C. | m+n=1 | D. | m+n=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 终边在x轴负半轴上的角是零角 | |
| B. | 三角形的内角必是第一、二象限内的角 | |
| C. | 不相等的角的终边一定不相同 | |
| D. | 若β=α+k•360°(k∈Z),则α与β终边相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
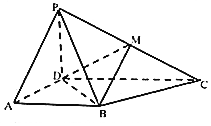 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是正三角形,底面ABCD是直角梯形,AB∥CD,CD⊥AD,CD=2AB=2AD=2,M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是正三角形,底面ABCD是直角梯形,AB∥CD,CD⊥AD,CD=2AB=2AD=2,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
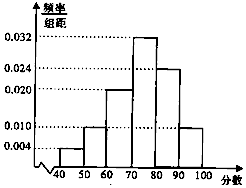 某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com