
【题目】已知函数f(x)=sinωx+cosωx(ω>0),x∈R,若函数f(x)在区间(﹣ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为 .
【答案】![]()
【解析】解:∵f(x)=sinωx+cosωx= ![]() sin(ωx+
sin(ωx+ ![]() ), ∵函数f(x)在区间(﹣ω,ω)内单调递增,ω>0
), ∵函数f(x)在区间(﹣ω,ω)内单调递增,ω>0
∴2kπ﹣ ![]() ≤ωx+
≤ωx+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z可解得函数f(x)的单调递增区间为:[
,k∈Z可解得函数f(x)的单调递增区间为:[ ![]() ,
, ![]() ],k∈Z,
],k∈Z,
∴可得:﹣ω≥ ![]() ①,ω≤
①,ω≤ ![]() ②,k∈Z,
②,k∈Z,
∴解得:0<ω2≤ ![]() 且0<ω2≤2k
且0<ω2≤2k ![]() ,k∈Z,
,k∈Z,
解得:﹣ ![]()
![]() ,k∈Z,
,k∈Z,
∴可解得:k=0,
又∵由ωx+ ![]() =kπ+
=kπ+ ![]() ,可解得函数f(x)的对称轴为:x=
,可解得函数f(x)的对称轴为:x= ![]() ,k∈Z,
,k∈Z,
∴由函数y=f(x)的图象关于直线x=ω对称,可得:ω2= ![]() ,可解得:ω=
,可解得:ω= ![]() .
.
故答案为: ![]() .
.
由两角和的正弦函数公式化简解析式可得f(x)= ![]() sin(ωx+
sin(ωx+ ![]() ),由2kπ﹣
),由2kπ﹣ ![]() ≤ωx+
≤ωx+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z可解得函数f(x)的单调递增区间,结合已知可得:﹣ω≥
,k∈Z可解得函数f(x)的单调递增区间,结合已知可得:﹣ω≥ ![]() ①,ω≤
①,ω≤ ![]() ②,k∈Z,从而解得k=0,又由ωx+
②,k∈Z,从而解得k=0,又由ωx+ ![]() =kπ+
=kπ+ ![]() ,可解得函数f(x)的对称轴为:x=
,可解得函数f(x)的对称轴为:x= ![]() ,k∈Z,结合已知可得:ω2=
,k∈Z,结合已知可得:ω2= ![]() ,从而可求ω的值.
,从而可求ω的值.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】上面图给出的是计算1+2+4+…+22017的值的一个程序框图,则其中判断框内应填入的是( ) 
A.i=2017?
B.i≥2017?
C.i≥2018?
D.i≤2018?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  .
.
(1)判断函数f(x)在区间(0,1)和[1,+∞)上的单调性(不必证明);
(2)当0<a<b,且f(a)=f(b)时,求 ![]() 的值;
的值;
(3)若存在实数a,b(1<a<b)使得x∈[a,b]时,f(x)的取值范围是[ma,mb](m≠0),求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A﹣BCD中,AB⊥平面BCD,CD⊥BD. 
(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A﹣MBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积. 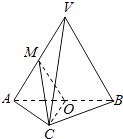
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +y2=1. (Ⅰ)求椭圆C的长轴和短轴的长,离心率e,左焦点F1;
+y2=1. (Ⅰ)求椭圆C的长轴和短轴的长,离心率e,左焦点F1;
(Ⅱ)经过椭圆C的左焦点F1作直线l,直线l与椭圆C相交于A,B两点,若|AB|= ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com