
分析 (1)利用有理数指数幂的性质、运算法则求解.
(2)利用有理数指数幂的性质、运算法则求解.
解答 解:(1)∵s>0,t>0,
∴$(\frac{{8{s^6}{t^{-3}}}}{{125{r^9}}}{)^{-\frac{2}{3}}}$=[($\frac{2{s}^{2}{t}^{-1}}{5{r}^{3}}$)3]${\;}^{-\frac{2}{3}}$
=($\frac{2{s}^{2}{t}^{-1}}{5{r}^{3}}$)-2=$\frac{25{r}^{6}{t}^{2}}{4{s}^{4}}$.
(2)∵x>0,y>0,
∴$(3{x^{\frac{1}{4}}}+2{y^{-\frac{1}{2}}})(3{x^{\frac{1}{4}}}-2{y^{-\frac{1}{2}}})$=($3{x}^{\frac{1}{4}}$)2-($2{y}^{-\frac{1}{2}}$)2=9x${\;}^{\frac{1}{2}}$-4y-1.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意有理数指数幂的性质、运算法则的合理运用.


科目:高中数学 来源: 题型:选择题
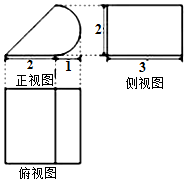
| A. | 4+$\frac{3}{2}$π | B. | 6+$\frac{3}{2}$π | C. | 6+3π | D. | 12+$\frac{3}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
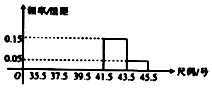 某商场为了了解某日旅游鞋的销售情况,抽取了部分顾客所购鞋的尺寸,将所得数据整理后,画出频率分布直方图如图所示.已知从左到右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分布如图所示,第2小组的频数为10,则第4小组顾客的人数是( )
某商场为了了解某日旅游鞋的销售情况,抽取了部分顾客所购鞋的尺寸,将所得数据整理后,画出频率分布直方图如图所示.已知从左到右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分布如图所示,第2小组的频数为10,则第4小组顾客的人数是( )| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 终边在x轴上角的集合是{α|α=kπ,k∈Z} | |
| B. | 终边在y轴上角的集合是$\{α|α=\frac{π}{2}+kπ,k∈Z\}$ | |
| C. | 终边在坐标轴上的角的集合是$\{α|α=k•\frac{π}{2},k∈Z\}$ | |
| D. | 终边在直线y=-x上角的集合是 $\{α|α=\frac{π}{4}+2kπ,k∈Z\}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com