
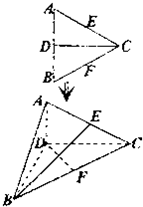
 在正△ABC中,CD为AB边上的高,E、F分别为边AC、BC的中点,将△ABC沿CD翻折成直二面角A-DC-B(如图),则异面直2,4,6线BE与DF所成的角为( )
在正△ABC中,CD为AB边上的高,E、F分别为边AC、BC的中点,将△ABC沿CD翻折成直二面角A-DC-B(如图),则异面直2,4,6线BE与DF所成的角为( ) 解:以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,设正△ABC的边长为4,
解:以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,设正△ABC的边长为4,| 3 |
| 3 |
| 3 |
| BE |
| 3 |
| DF |
| 3 |
| BE |
| DF |
| ||||
|
|
| -2+3 | ||
2
|
| ||
| 8 |
| ||
| 8 |


科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:单选题




查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省张家界市高三(上)一轮复习数学专项训练:直线、平面垂直的判定与性质(解析版) 题型:选择题





查看答案和解析>>
科目:高中数学 来源:2009-2010学年云南省曲靖市罗平县高三(下)复习适应性检测数学试卷(文科)(解析版) 题型:选择题
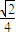

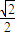

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com