
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 的单调性.
的单调性.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1) 欲求在点(2,f(2))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决;
(2)求出![]() ,对a分类讨论,解不等式即可得到
,对a分类讨论,解不等式即可得到![]() 的单调性与极值点.
的单调性与极值点.
(1)当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,
,
所以所求切线的斜率为![]() .
.
故所求的切线方程为![]() ,即
,即![]() .
.
(2)![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
①当![]() 时,
时,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
②当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() .
.
(i)当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(ii)当![]() 时,
时,![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增.
上单调递增.
(iii)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为节能环保,推进新能源汽车推广和应用,对购买纯电动汽车的用户进行财政补贴,财政补贴由地方财政补贴和国家财政补贴两部分组成. 某地补贴政策如下(![]() 表示纯电续航里程):
表示纯电续航里程):
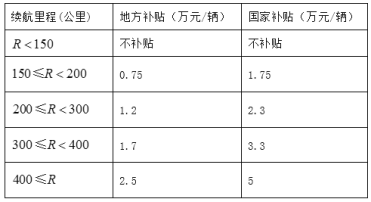
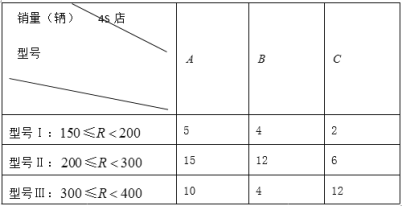
有![]() 三个纯电动汽车
三个纯电动汽车![]() 店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下:
店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下:
(每位客户只能购买一辆纯电动汽车)
(1)从上述购买纯电动汽车的客户中随机选一人,求此人购买的是![]() 店纯电动汽车且享受补贴不低于3.5万元的概率;
店纯电动汽车且享受补贴不低于3.5万元的概率;
(2)从上述![]() 两个纯电动汽车
两个纯电动汽车![]() 店的客户中各随机选一人,求恰有一人享受5万元财政补贴的概率;
店的客户中各随机选一人,求恰有一人享受5万元财政补贴的概率;
(3)从上述![]() 三个纯电动汽车
三个纯电动汽车![]() 店的客户中各随机选一人, 这3个人享受的财政补贴分别记为
店的客户中各随机选一人, 这3个人享受的财政补贴分别记为![]() . 求随机变量
. 求随机变量![]() 的分布列. 试比较数学期望
的分布列. 试比较数学期望![]() 的大小;比较方差
的大小;比较方差![]()
![]() 的大小. (只需写出结论)
的大小. (只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】洛萨![]() 科拉茨
科拉茨![]() Collatz,
Collatz,![]() 是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半
是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半![]() 即
即![]() ;如果n是奇数,则将它乘3加
;如果n是奇数,则将它乘3加![]() 即
即![]() ,不断重复这样的运算,经过有限步后,一定可以得到
,不断重复这样的运算,经过有限步后,一定可以得到![]() 如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,
如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,![]() 对科拉茨
对科拉茨![]()
![]() 猜想,目前谁也不能证明,更不能否定
猜想,目前谁也不能证明,更不能否定![]() 现在请你研究:如果对正整数
现在请你研究:如果对正整数![]() 首项
首项![]() 按照上述规则施行变换
按照上述规则施行变换![]() 注:1可以多次出现
注:1可以多次出现![]() 后的第八项为1,则n的所有可能的取值为______.
后的第八项为1,则n的所有可能的取值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】洛萨![]() 科拉茨
科拉茨![]() Collatz,
Collatz,![]() 是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半
是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半![]() 即
即![]() ;如果n是奇数,则将它乘3加
;如果n是奇数,则将它乘3加![]() 即
即![]() ,不断重复这样的运算,经过有限步后,一定可以得到
,不断重复这样的运算,经过有限步后,一定可以得到![]() 如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,
如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,![]() 对科拉茨
对科拉茨![]()
![]() 猜想,目前谁也不能证明,更不能否定
猜想,目前谁也不能证明,更不能否定![]() 现在请你研究:如果对正整数
现在请你研究:如果对正整数![]() 首项
首项![]() 按照上述规则施行变换
按照上述规则施行变换![]() 注:1可以多次出现
注:1可以多次出现![]() 后的第八项为1,则n的所有可能的取值为______.
后的第八项为1,则n的所有可能的取值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐,奖牌榜的前3名如下:
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某数学爱好者采用分层抽样的方式,从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人, 则这3人中中国选手恰好1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人玩摸球游戏,每两局为一轮,每局游戏的规则如下:甲,乙两人均从装有4只红球、1只黑球的袋中轮流不放回摸取1只球,摸到黑球的人获胜,并结束该局.
(1)若在一局中甲先摸,求甲在该局获胜的概率;
(2)若在一轮游戏中约定:第一局甲先摸,第二局乙先摸,每一局先摸并获胜的人得1分,后摸井获胜的人得2分,未获胜的人得0分,求此轮游戏中甲得分X的概率分布及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com