
 的递增区间是
的递增区间是 ;
; )<f(a+
)<f(a+ );
); 的图象关于点
的图象关于点 对称;
对称; 是函数
是函数 图象的一条对称轴;
图象的一条对称轴; 的图象向右平移
的图象向右平移 个单位得到.
个单位得到. )>f(a+
)>f(a+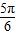 ),判断②正误.
),判断②正误.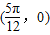 在函数图象上,结合图象可得函数图象关于点
在函数图象上,结合图象可得函数图象关于点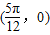 )对称,判断③的正误.
)对称,判断③的正误.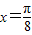 ,函数取得最值,即可判断正误.
,函数取得最值,即可判断正误. -3x)=cos(3x-
-3x)=cos(3x-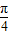 ),根据余弦函数的增区间是[2kπ-π,2kπ],k∈z,
),根据余弦函数的增区间是[2kπ-π,2kπ],k∈z,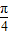 ≤2kπ+
≤2kπ+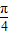 ,解得
,解得  kπ-
kπ-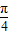 ≤x≤
≤x≤ kπ+
kπ+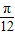 ,k∈Z,故①正确.
,k∈Z,故①正确.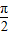 ,a+
,a+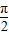 ]上是单调增函数.
]上是单调增函数. )=f(a-
)=f(a-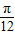 ),f(a+
),f(a+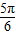 )=f(a-
)=f(a-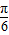 ),a-
),a-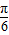 <a-
<a-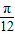 ,
,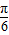 )<f( a-
)<f( a-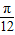 ),即 f(a+
),即 f(a+ )>f(a+
)>f(a+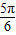 );故②不正确.
);故②不正确.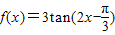 ,由于点
,由于点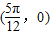 在图象上,结合图象可得函数图象关于点
在图象上,结合图象可得函数图象关于点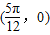 对称,
对称,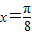 代入函数
代入函数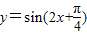 ,函数取得最大值,所以
,函数取得最大值,所以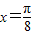 是函数图象的一条对称轴,故④正确.
是函数图象的一条对称轴,故④正确.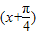 的图象向右平移
的图象向右平移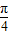 个单位,得到函数y=sinx的图象,故⑤不正确.
个单位,得到函数y=sinx的图象,故⑤不正确.

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| 2kπ |
| 3 |
| π |
| 12 |
| 2kπ |
| 3 |
| π |
| 12 |
| 5π |
| 6 |
| π |
| 3 |
| 5π |
| 12 |
| π |
| 8 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| 2kπ |
| 3 |
| π |
| 12 |
| 2kπ |
| 3 |
| π |
| 12 |
| 5π |
| 6 |
| π |
| 3 |
| 5π |
| 12 |
| π |
| 3 |
| π |
| 3 |
| x |
| 2 |
| 3π |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省吉安市白鹭洲中学高三(上)第二次月考数学试卷(文科)(解析版) 题型:选择题
 的递增区间是
的递增区间是 ;
; )<f(a+
)<f(a+ );
); 的图象关于点
的图象关于点 对称;
对称; 是函数
是函数 图象的一条对称轴;
图象的一条对称轴; 的图象向右平移
的图象向右平移 个单位得到.
个单位得到.查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省扬州中学高一(上)期末数学试卷(解析版) 题型:填空题
 的递增区间是
的递增区间是 ;
; ;
;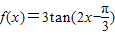 的图象关于点
的图象关于点 对称;
对称; 的图象向右平移
的图象向右平移 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象; 的图象和直线
的图象和直线 的交点个数是1个.
的交点个数是1个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com