
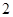 的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=
的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=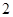 .
.
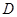 到平面
到平面 的距离.
的距离.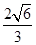 。
。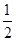 PD……………………………….3
PD……………………………….3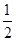 PD,
PD,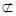 平面ABCD,且
平面ABCD,且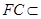 平面ABCD 所以EN//平面ABCD;………………….6
平面ABCD 所以EN//平面ABCD;………………….6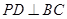 ,且
,且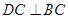 ,故
,故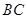 是三棱锥
是三棱锥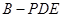 的高,
的高,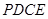 中,可求得
中,可求得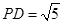 ,且
,且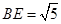 由(1)所以
由(1)所以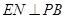 ………9
………9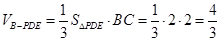 ,…………………11
,…………………11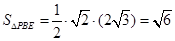 ,…………………………12
,…………………………12 ,则
,则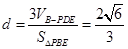 ……………..14
……………..14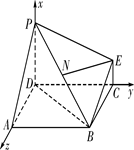 ………………………………1,
………………………………1,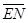 =(1,-1,0),
=(1,-1,0), 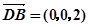 ……………………..3
……………………..3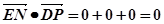
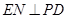 ,…………… ……………4
,…………… ……………4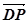 是平面ABCD的法向量
是平面ABCD的法向量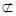 平面ABCD 所以EN//平面ABCD;……………………………….6
平面ABCD 所以EN//平面ABCD;……………………………….6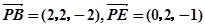 ,…………….8
,…………….8 的法向量为
的法向量为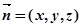
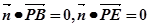 得
得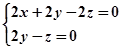 …………………. ……………10
…………………. ……………10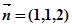 ………………………..11
………………………..11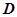 到平面
到平面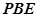 的距离为
的距离为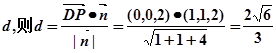 ……14
……14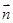 为α的一个法向量,则点A到平面α的距离
为α的一个法向量,则点A到平面α的距离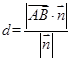 。
。

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:不详 题型:单选题
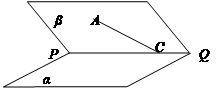
| A.1 | B.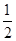 | C.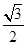 | D.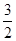 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
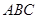 为底面的直棱柱被平面
为底面的直棱柱被平面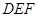 所截而得.
所截而得. 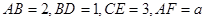 ,
,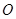 为
为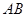 的中点.
的中点.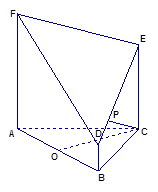
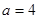 时,求平面
时,求平面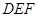 与平面
与平面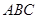 的夹角的余弦值;
的夹角的余弦值;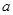 为何值时,在棱
为何值时,在棱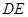 上存在点
上存在点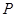 ,使
,使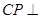 平面
平面 ?
?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.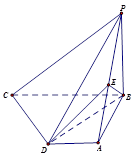
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 是直线,a、β是平面,给出下列命题:
是直线,a、β是平面,给出下列命题: 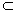 α,l
α,l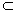 β,且l⊥m,则α⊥β;
β,且l⊥m,则α⊥β;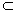 β,且l⊥α,则α⊥β;
β,且l⊥α,则α⊥β;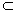 α,l
α,l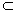 β,且α∥β,则l∥m.
β,且α∥β,则l∥m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com