
 如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.
如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.
 | |||
 | |||
(Ⅰ)见解析 (Ⅱ) arccos![]() (Ⅲ)
(Ⅲ)![]()
(Ⅰ)∵AB = 3,BC = 4,∴AC = 5
∵AC2 = AB2 + BC2,∴AB⊥BC,又AB⊥BB1,
 且BC∩BB1 = B,∴AB⊥面BCC1B1 ; (4分)
且BC∩BB1 = B,∴AB⊥面BCC1B1 ; (4分)
(Ⅱ)如图,建立空间直角坐标系
则A(3,0,0),P(0,0,3),Q(0,4,4)
设面APQ的法向量为![]() = (x,y,z)
= (x,y,z)
![]()
![]()
![]() = (1,–1,1)而面ABC的法向量可以取
= (1,–1,1)而面ABC的法向量可以取![]() = (0,0,1)
= (0,0,1)
∴![]() ∴面PQA与面ABC所成的锐二面角
∴面PQA与面ABC所成的锐二面角
为arccos![]() . (8分)
. (8分)
(Ⅲ)∵BP = AB = 3,CQ = AC = 7.∴S四边形BCQP =![]()
∴VA—BCQP =![]() ×20×3 = 20又∵V
×20×3 = 20又∵V![]() =
=![]() .
.
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年山西省高三1月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图,在边长为4的菱形 中,
中, .点
.点 分别在边
分别在边 上,点
上,点 与点
与点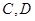 不重合,
不重合, ,
, .沿
.沿 将
将 翻折到
翻折到 的位置,使平面
的位置,使平面 ⊥平面
⊥平面 .
.

(1)求证: ⊥平面
⊥平面 ;
;
(2)当 取得最小值时,请解答以下问题:
取得最小值时,请解答以下问题:
(i)求四棱锥 的体积;
的体积;
(ii)若点 满足
满足 =
=
 (
( ),试探究:直线
),试探究:直线 与平面
与平面 所成角的大小是否一定大于
所成角的大小是否一定大于 ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三下学期第一次月考考试数学理卷 题型:解答题
(本小题满分12分)
如图,在边长为a的正方体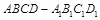 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、 、
、 的中点.
的中点.
(1)求点P到平面MNQ的距离;
(2)求直线PN与平面MPQ所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
如图,在边长为25cm的正方形中挖去直角边长分别为23cm和2cm的四个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是多少?
 |
查看答案和解析>>
科目:高中数学 来源:云南省曲靖一中08-09学年高二下学期期末考试(数学理) 题型:选择题
(由理科第三册§3.8例2及文科第三册§2.5例2改编)如图,在边长为6cm的正方形铁皮的四角截去相等的正方形,将剩余部分沿虚线折起,做成无盖方底箱子,这个箱子的最大容积是( )

A.12 cm3 B.16 cm3 C.24cm3 D.36 cm3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com