
【题目】如图,要在河岸![]() 的一侧修建一条休闲式人行道,进行图纸设计时,建立了图中所示坐标系,其中
的一侧修建一条休闲式人行道,进行图纸设计时,建立了图中所示坐标系,其中![]() ,
,![]() 在
在![]() 轴上,且
轴上,且![]() ,道路的前一部分为曲线段
,道路的前一部分为曲线段![]() ,该曲线段为二次函数
,该曲线段为二次函数![]() 在
在![]() 时的图像,最高点为
时的图像,最高点为![]() ,道路中间部分为直线段
,道路中间部分为直线段![]() ,
,![]() ,且
,且![]() ,道路的后一段是以
,道路的后一段是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.
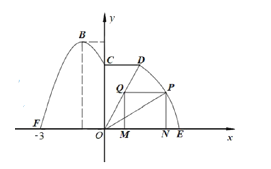
(1)求![]() 的值;
的值;
(2)求![]() 的大小;
的大小;
(3)若要在扇形区域![]() 内建一个“矩形草坪”
内建一个“矩形草坪”![]() ,
,![]() 在圆弧
在圆弧![]() 上运动,
上运动,![]() 、
、![]() 在
在![]() 上,记
上,记![]() ,则当
,则当![]() 为何值时,“矩形草坪”面积最大.
为何值时,“矩形草坪”面积最大.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.

(1)求这200名学生每周阅读时间的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该校学生每周的阅读时间![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() .利用直方图得到的正态分布,求
.利用直方图得到的正态分布,求![]() .
.
(ii)从该高校的学生中随机抽取20名,记![]() 表示这20名学生中每周阅读时间超过10小时的人数,求
表示这20名学生中每周阅读时间超过10小时的人数,求![]() (结果精确到0.0001)以及
(结果精确到0.0001)以及![]() 的数学期望.
的数学期望.
参考数据:![]() ,
,![]() .若
.若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换 得到曲线,设M(x,y)为
得到曲线,设M(x,y)为![]() 上任意一点,求
上任意一点,求![]() 的最小值,并求相应的点M的坐标.
的最小值,并求相应的点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,点P是椭圆上的任意一点,且
,点P是椭圆上的任意一点,且![]() 的最大值为4,椭圆C的离心率与双曲线
的最大值为4,椭圆C的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设点
设点![]() ,过点P作两条直线
,过点P作两条直线![]() ,
,![]() 与圆
与圆![]() 相切且分别交椭圆于M,N,求证:直线MN的斜率为定值.
相切且分别交椭圆于M,N,求证:直线MN的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
![]() 根据上面图表,求
根据上面图表,求![]() 处的数值
处的数值
![]() 在所给的坐标系中画出
在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
![]() 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() .
.![]() 为
为![]() 的中点.
的中点.

(1)若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)当平面![]() 平面
平面![]() 时,线段
时,线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ?若存在,求出点
?若存在,求出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 1(a>0)的中心为原点O,左、右焦点分别为F1、F2,离心率为
1(a>0)的中心为原点O,左、右焦点分别为F1、F2,离心率为![]() ,点P是直线x
,点P是直线x![]() 上任意一点,点Q在椭圆E上,且满足
上任意一点,点Q在椭圆E上,且满足![]() 0.
0.
(1)试求出实数a;
(2)设直线PQ与直线OQ的斜率分别为k1与k2,求积k1k2的值;
(3)若点P的纵坐标为1,过点P作动直线l与椭圆交于不同的两点M、N,在线段MN上取异于点M、N的点H,满足![]() ,证明点H恒在一条定直线上.
,证明点H恒在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①设A,B为两个集合,则“![]() ”是“
”是“![]() ”的充分不必要条件;②
”的充分不必要条件;②![]() ,
,![]() ;③“
;③“![]() ”是“
”是“![]() ”的充要条件;④
”的充要条件;④![]() ,代数式
,代数式![]() 的值都是质数.其中的真命题是________.(填写序号)
的值都是质数.其中的真命题是________.(填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com