
【题目】已知实数对(x,y),设映射f:(x,y)→( ![]() ,
, ![]() ),并定义|(x,y)|=
),并定义|(x,y)|= ![]() ,若|f[f(f(x,y))]|=8,则|(x,y)|的值为( )
,若|f[f(f(x,y))]|=8,则|(x,y)|的值为( )
A.4 ![]()
B.8 ![]()
C.16 ![]()
D.32 ![]()
【答案】C
【解析】解:∵映射f:(x,y)→( ![]() ,
, ![]() ),
),
∴f[f(f(x,y))]=f(f( ![]() ,
, ![]() ))=f(
))=f( ![]() ,
, ![]() )=(
)=( ![]() ,
, ![]() ),
),
∵定义|(x,y)|= ![]() ,若|f[f(f(x,y))]|=8,
,若|f[f(f(x,y))]|=8,
∴|( ![]() ,
, ![]() )|=8,
)|=8,
∴ ![]() =8,
=8,![]()
∴|(x,y)|的值为16 ![]() ,
,
故选:C
【考点精析】解答此题的关键在于理解映射的相关定义的相关知识,掌握对于映射f:A→B来说,则应满足:(1)集合A中的每一个元素,在集合B中都有象,并且象是唯一的;(2)集合A中不同的元素,在集合B中对应的象可以是同一个;(3)不要求集合B中的每一个元素在集合A中都有原象;注意:映射是针对自然界中的所有事物而言的,而函数仅仅是针对数字来说的.所以函数是映射,而映射不一定的函数.


科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程![]() =0.
=0.
(1)若a是从集合A={x∈Z|0≤x≤3}中任取一个元素,b是从集合B={x∈Z|0≤x≤2}中任取一个元素,求方程![]() =0恰有两个不相等实根的概率;
=0恰有两个不相等实根的概率;
(2) 若a是从集合A={x|0≤x≤3}中任取一个元素,b是从集合B={x|0≤x≤2}中任取一个元素,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且cos2 ![]() =
= ![]() ,△ABC的面积为4.
,△ABC的面积为4.
(1)求 ![]() 的值;
的值;
(2)若2sinB=5sinC,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2是椭圆C的左右焦点,点A,B为其左右顶点,P为椭圆C上(异于A、B)的一动点,当P点坐标为(1, ![]() )时,△PF1F2的面积为
)时,△PF1F2的面积为 ![]() ,分别过点A、B、P作椭圆C的切线l1 , l2 , l,直线l与l1 , l2分别交于点R,T.
,分别过点A、B、P作椭圆C的切线l1 , l2 , l,直线l与l1 , l2分别交于点R,T. 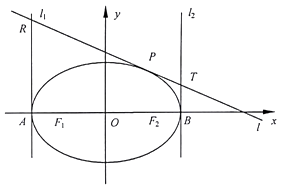
(1)求椭圆C的方程;
(2)(i)求证:以RT为直径的圆过定点,并求出定点M的坐标;
(ii)求△RTM的面积最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列4个命题,其中正确命题的个数是( )
①计算:9192除以100的余数是1;
②命题“x>0,x﹣lnx>0”的否定是“x>0,x﹣lnx≤0”;
③y=tanax(a>0)在其定义域内是单调函数而且又是奇函数;
④命题p:“|a|+|b|≤1”是命题q:“对任意的x∈R,不等式asinx+bcosx≤1恒成立”的充分不必要条件.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市自来水公司每两个月(记为一个收费周期)对用户收一次水费,收费标准如下:当每户用水量不超过![]() 吨时,按每吨
吨时,按每吨![]() 元收取;当该用户用水量超过
元收取;当该用户用水量超过![]() 吨时,超出部分按每吨
吨时,超出部分按每吨![]() 元收取.
元收取.
(1)记某用户在一个收费周期的用水量为![]() 吨,所缴水费为
吨,所缴水费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)在某一个收费周期内,若甲、乙两用户所缴水费的和为![]() 元,且甲、乙两用户用水量之比为
元,且甲、乙两用户用水量之比为![]() ,试求出甲、乙两用户在该收费周期内各自的用水量和水费.
,试求出甲、乙两用户在该收费周期内各自的用水量和水费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com