
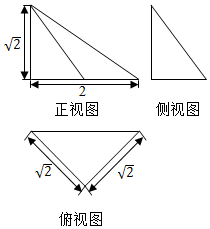
 一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为23cm2,该该几何体的体积为$\frac{23}{3}$cm3.
一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为23cm2,该该几何体的体积为$\frac{23}{3}$cm3. 分析 由三视图知该几何体是一个正方体截去一个三棱锥所得的组合体,由正方体的性质求出棱长,由面积公式求出几何体的表面积;根据柱体、椎体的体积公式求出该几何体的体积.
解答 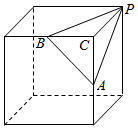 解:根据三视图可知几何体是:
解:根据三视图可知几何体是:
一个正方体截去一个三棱锥P-ABC所得的组合体,
直观图如图所示:其中A、B是棱的中点,
正方体的棱长是2cm,则PA=PB=$\sqrt{5}$cm,AB=$\sqrt{2}$cm,
∴△PAB边AB上的高线为$\sqrt{(\sqrt{5})^{2}-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{3\sqrt{2}}{2}$(cm),
∴该几何体的表面积:
S=$6×2×2-2×\frac{1}{2}×1×2-\frac{1}{2}×1×1+\frac{1}{2}×\sqrt{2}×\frac{3\sqrt{2}}{2}$
=23(cm2),
该几何体的体积V=$2×2×2-\frac{1}{3}×\frac{1}{2}×1×1×2$=$\frac{23}{3}$(cm3),
故答案为:23cm2;$\frac{23}{3}$cm3.
点评 本题考查由三视图求几何体的体积以及表面积,由三视图正确复原几何体是解题的关键,考查空间想象能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (-∞,-2)∪(2,+∞) | C. | (-1,2) | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2+2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com