
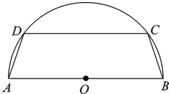
 有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.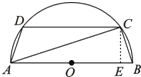

 =
=
 =
=


 (6分)
(6分)
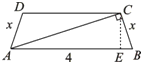
 =4-
=4- y=4+2x+4-
y=4+2x+4-
 +2x+8(0<x<2
+2x+8(0<x<2 )
) ,CD=4-2×
,CD=4-2× =
= ,从而可求
,从而可求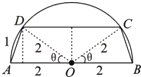


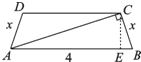

 =4-
=4- y=4+2x+4-
y=4+2x+4-
 +2x+8(0<x<2
+2x+8(0<x<2 ),利用二次函数的知识可求.
),利用二次函数的知识可求.

科目:高中数学 来源: 题型:
 如图,半圆形公园上有P和Q两点,线段AB是该半圆的一条直径,C为圆心,半径是2km,现要在公园内建一块顶点都在半圆C上的多边形活动场地为等腰梯形ABPQ.
如图,半圆形公园上有P和Q两点,线段AB是该半圆的一条直径,C为圆心,半径是2km,现要在公园内建一块顶点都在半圆C上的多边形活动场地为等腰梯形ABPQ.查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
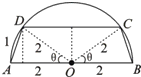
如图所示,有一块半径为R的半圆型钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是圆O的直径,上底CD的端点在圆周上,
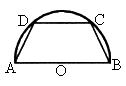
(1)若梯形的腰长为x,求其上底长;
(2)写出梯形的周长y以腰长x为自变量的函数解析式,并求出其定义域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com