
【题目】已知圆![]() 经过两点
经过两点![]() ,
,![]() ,且圆心
,且圆心![]() 在直线
在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,点
两点,点![]() 为圆
为圆![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 交
交![]() 轴于
轴于![]() 、
、![]() 点.当点
点.当点![]() 变化时,以
变化时,以![]() 为直径的圆
为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论.
内一定点?请证明你的结论.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】小张举办了一次抽奖活动.顾客花费3元钱可获得一次抽奖机会.每次抽奖时,顾客从装有1个黑球,3个红球和6个白球(除颜色外其他都相同)的不透明的袋子中依次不放回地摸出3个球,根据摸出的球的颜色情况进行兑奖.顾客中一等奖,二等奖,三等奖,四等奖时分别可领取的奖金为![]() 元,10元,5元,1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:
元,10元,5元,1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:![]() 个黑球2个红球;
个黑球2个红球;![]() 个红球;
个红球;![]() 恰有1个白球;
恰有1个白球;![]() 恰有2个白球;
恰有2个白球;![]() 个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖,中二等奖,中三等奖,中四等奖,不中奖.
个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖,中二等奖,中三等奖,中四等奖,不中奖.
(1)通过计算写出中一至四等奖分别对应的情况(写出字母即可);
(2)已知顾客摸出的第一个球是红球,求他获得二等奖的概率;
(3)设顾客抽一次奖小张获利![]() 元,求变量
元,求变量![]() 的分布列;若小张不打算在活动中亏本,求
的分布列;若小张不打算在活动中亏本,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]()
![]() =
=![]() (
(![]() >0),过点
>0),过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线![]() 与曲线C相交于A,B两点.
与曲线C相交于A,B两点.
(Ⅰ)写出曲线C的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线与抛物线交于
的直线与抛物线交于![]() 两点,且
两点,且![]() ,抛物线的准线
,抛物线的准线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 于点
于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() ,过
,过![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 两点,且
两点,且![]() ,点
,点![]() 为线段
为线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点,则点
轴的交点,则点![]() 的横坐标
的横坐标![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,四边形
中,四边形![]() 为菱形,
为菱形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 在线段
在线段![]() 上移动,
上移动,![]() 为棱
为棱![]() 的中点.
的中点.
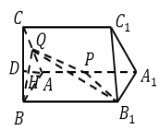
(1)若![]() 为线段
为线段![]() 的中点,
的中点,![]() 为
为![]() 中点,延长
中点,延长![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象相邻两条对称轴之间的距离为
图象相邻两条对称轴之间的距离为![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到的图象关于
个单位,得到的图象关于![]() 轴对称,则( )
轴对称,则( )
A. 函数![]() 的周期为
的周期为![]() B. 函数
B. 函数![]() 图象关于点
图象关于点![]() 对称
对称
C. 函数![]() 图象关于直线
图象关于直线![]() 对称 D. 函数
对称 D. 函数![]() 在
在![]() 上单调
上单调
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com