
°æƒø°ø“—÷™ ˝¡–{an}µƒ∏˜œÓæ˘Œ™’˝ ˝£¨∆‰«∞nœÓµƒ∫ÕŒ™Sn£¨«“∂‘»Œ“‚µƒm£¨n° N*£¨
∂º”–(Sm£´n£´S1)2£Ω4a2ma2n£Æ
£®1£©«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©«Û÷§£∫{an}Œ™µ»±» ˝¡–£ª
£®3£©“—÷™ ˝¡–{cn}£¨{dn}¬˙◊„|cn|£Ω|dn|£Ωan£¨p(p°ð3) «∏¯∂®µƒ’˝’˚ ˝£¨ ˝¡–{cn}£¨{dn}µƒ«∞pœÓµƒ∫Õ∑÷±Œ™Tp£¨Rp£¨«“Tp£ΩRp£¨«Û÷§£∫∂‘»Œ“‚’˝’˚ ˝k(1°Ðk°Ðp)£¨ck£Ωdk£Æ
°æ¥∞∏°ø£®1£©2£ª£®2£©º˚Ω‚Œˆ£ª£®3£©º˚Ω‚Œˆ.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©±æÂ≤…”√∏≥÷µ∑®£¨‘⁄“—÷™µ» Ω÷–¡Ó![]() µ√µ√≥ˆ
µ√µ√≥ˆ![]() µƒπÿœµ£ª£®2£©“≤≤…”√∏≥÷µ∑®£¨±æƒ—µ„‘⁄”⁄“—÷™Ãıº˛÷–µƒ∆Ω∑Ωµƒ¥¶¿Ì£¨Œ™¥Àœ»»°
µƒπÿœµ£ª£®2£©“≤≤…”√∏≥÷µ∑®£¨±æƒ—µ„‘⁄”⁄“—÷™Ãıº˛÷–µƒ∆Ω∑Ωµƒ¥¶¿Ì£¨Œ™¥Àœ»»°![]() ∫Õ
∫Õ![]() £¨À˘µ√¡Ω¡™¡¢Ω·∫œ£®1£©ø…µ√
£¨À˘µ√¡Ω¡™¡¢Ω·∫œ£®1£©ø…µ√![]() £¨»ª∫Û¡Ó
£¨»ª∫Û¡Ó![]() µ√
µ√![]() £¨¡Ó
£¨¡Ó![]() µ√
µ√![]() £¨¥À¡Ω Ωœý≥˝µ√
£¨¥À¡Ω Ωœý≥˝µ√ £¨“Ú¥À
£¨“Ú¥À £¨º¥
£¨º¥![]() £¨œ¬√Ê¥¶¿Ì∑Ω∑®¥Ûº“”¶∏√∫ЫÂ≥˛¡À£¨”…¥À Ω”–
£¨œ¬√Ê¥¶¿Ì∑Ω∑®¥Ûº“”¶∏√∫ЫÂ≥˛¡À£¨”…¥À Ω”–![]() £¨œý”¶¡Ω Ωœýºıø…÷§µ√Ω·¬€£ª£®3£©”√∑¥÷§∑®÷§√˜£¨”…£®1£©
£¨œý”¶¡Ω Ωœýºıø…÷§µ√Ω·¬€£ª£®3£©”√∑¥÷§∑®÷§√˜£¨”…£®1£©![]() £¨»Ù
£¨»Ù![]() £¨≤ª∑¡…Ë
£¨≤ª∑¡…Ë![]() £¨
£¨ ![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨ ![]() £¨’‚”Γ—÷™Tp£ΩRp√¨∂У¨¥”∂¯
£¨’‚”Γ—÷™Tp£ΩRp√¨∂У¨¥”∂¯![]() £¨”⁄ «
£¨”⁄ «![]() £¨‘Ú
£¨‘Ú![]() £¨“¿¥Œø…÷§√˜Ã‚…ËΩ·¬€.
£¨“¿¥Œø…÷§√˜Ã‚…ËΩ·¬€.
‘Ã‚Ω‚Œˆ£∫£®1£©”…(Sm£´n£´S1)2£Ω4a2na2m£¨µ√(S2£´S1)2£Ω4a£¨º¥(a2£´2a1)2£Ω4a£Æ
“ÚŒ™a1£æ0£¨a2£æ0£¨À˘“‘a2£´2a1£Ωa2£¨º¥£Ω2£Æ 3∑÷
÷§√˜£∫£®2£©£®∑Ω∑®“ª£©¡Óm£Ω1£¨n£Ω2£¨µ√(S3£´S1)2£Ω4a2a4£¨º¥(2a1£´a2£´a3)2£Ω4a2a4£¨
¡Óm£Ωn£Ω2£¨µ√S4£´S1£Ω2a4£¨º¥2a1£´a2£´a3£Ωa4£Æ
À˘“‘a4£Ω4a2£Ω8a1£Æ
”÷“ÚŒ™£Ω2£¨À˘“‘a3£Ω4a1£Æ 6∑÷
”…(Sm£´n£´S1)2£Ω4a2na2m£¨µ√(Sn£´1£´S1)2£Ω4a2na2£¨(Sn£´2£´S1)2£Ω4a2na4£Æ
¡Ω Ωœý≥˝£¨µ√£Ω£¨À˘“‘£Ω£Ω2£Æ
º¥Sn£´2£´S1£Ω2(Sn£´1£´S1)£¨
¥”∂¯Sn£´3£´S1£Ω2(Sn£´2£´S1)£Æ
À˘“‘an£´3£Ω2an£´2£¨π µ±n°ð3 ±£¨{an} «π´±»Œ™2µƒµ»±» ˝¡–£Æ
”÷“ÚŒ™a3£Ω2a2£Ω4a1£¨¥”∂¯an£Ωa1°§2 n£≠1£¨n° N*£Æ
œ‘»ª£¨an£Ωa1°§2 n£≠1¬˙◊„Â…Ë£¨
“Ú¥À{an} « ◊œÓŒ™a1£¨π´±»Œ™2µƒµ»±» ˝¡–£Æ 10∑÷
£®∑Ω∑®∂˛£©‘⁄(Sm£´n£´S1)2£Ω4a2na2m÷–£¨
¡Óm£Ωn£¨µ√S2n£´S1£Ω2a2n£Æ ¢Ÿ
¡Óm£Ωn£´1£¨µ√S2n£´1£´S1£Ω2£¨ ¢⁄
‘⁄¢Ÿ÷–£¨”√n£´1¥˙nµ√£¨S2n£´2£´S1£Ω2a2n£´2£Æ ¢€
¢⁄£≠¢Ÿ£¨µ√a2n£´1£Ω2£≠2a2n£Ω2(£≠)£¨ ¢Ð
¢€£≠¢⁄£¨µ√a2n£´2£Ω2a2n£´2£≠2£Ω2(£≠)£¨ ¢ð
”…¢Ð¢ðµ√a2n£´1£Ω£Æ ¢Þ 8∑÷
¢Þ¥˙»Î¢Ð£¨µ√a2n£´1£Ω2a2n£ª¢Þ¥˙»Î¢ðµ√a2n£´2£Ω2a2n£´1£¨
À˘“‘£Ω£Ω2£Æ”÷£Ω2£¨
¥”∂¯an£Ωa1°§2 n£≠1£¨n° N*£Æ
œ‘»ª£¨an£Ωa1°§2 n£≠1¬˙◊„Â…Ë£¨
“Ú¥À{an} « ◊œÓŒ™a1£¨π´±»Œ™2µƒµ»±» ˝¡–£Æ 10∑÷
£®3£©”…£®2£©÷™£¨an£Ωa1°§2 n£≠1£Æ
“ÚŒ™|cp|£Ω|dp|£Ωa1°§2p£≠1£¨À˘“‘cp£ΩdpªÚcp£Ω£≠dp£Æ
»Ùcp£Ω£≠dp£¨≤ª∑¡…Ëcp£æ0£¨dp£º0£¨
‘ÚTp°ða1°§2p£≠1£≠(a1°§2p£≠2£´a1°§2p£≠3£´ £´a1)£Ωa1°§2p£≠1£≠a1°§(2p£≠1£≠1)£Ωa1£æ0£Æ
Rp°Ð£≠a1°§2p£≠1£´(a1°§2p£≠2£´a1°§2p£≠3£´ £´a1)£Ω£≠a1°§2p£≠1£´a1°§(2p£≠1£≠1)£Ω£≠a1£º0£Æ
’‚”ÎTp£ΩRp√¨∂У¨À˘“‘cp£Ωdp£Æ
¥”∂¯Tp£≠1£ΩRp£≠1£Æ
”……œ÷§√˜£¨Õ¨¿Ìø…µ√cp£≠1£Ωdp£≠1£Æ»Á¥Àœ¬»•£¨ø…µ√cp£≠2£Ωdp£≠2£¨cp£≠3£Ωdp£≠3£Æ£¨c1£Ωd1£Æ
º¥∂‘»Œ“‚’˝’˚ ˝k(1°Ðk°Ðp)£¨ck£Ωdk£Æ 16∑÷



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨µ„PµΩ¡Ωµ„(0,-![]() )£¨(0,
)£¨(0,![]() )µƒæý¿Î÷Æ∫Õµ»”⁄4£¨…˵„PµƒπϺ£Œ™C£Æ
)µƒæý¿Î÷Æ∫Õµ»”⁄4£¨…˵„PµƒπϺ£Œ™C£Æ
£®1£©–¥≥ˆCµƒ∑Ω≥ãª
£®2£©…Ë÷±œþy=kx+1”ÎCΩª”⁄A°¢B¡Ωµ„£¨kŒ™∫Œ÷µ ±![]()
![]()
![]() £ø
£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥π´Àæ—–æøø™∑¢¡À“ª÷÷–¬≤˙∆∑£¨…˙≤˙’‚÷÷–¬≤˙∆∑µƒƒÍπÃ∂®≥…±æŒ™150ÕÚ‘™£¨√ø…˙≤˙![]() «ßº˛£¨–Ë¡ÌÕ∂»Î≥…±æŒ™
«ßº˛£¨–Ë¡ÌÕ∂»Î≥…±æŒ™![]() (ÕÚ‘™)£¨
(ÕÚ‘™)£¨ 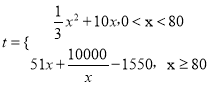 .√øº˛≤˙∆∑ €º€Œ™500‘™.∏√–¬≤˙∆∑‘⁄ –≥°…œπ©≤ª”¶«Ûø…»´≤ø¬ÙÕÍ.
.√øº˛≤˙∆∑ €º€Œ™500‘™.∏√–¬≤˙∆∑‘⁄ –≥°…œπ©≤ª”¶«Ûø…»´≤ø¬ÙÕÍ.
£®¢Ò£©–¥≥ˆƒÍ¿˚»Û![]() £®ÕÚ‘™£©πÿ”⁄ƒÍ≤˙¡ø
£®ÕÚ‘™£©πÿ”⁄ƒÍ≤˙¡ø![]() £®«ßº˛£©µƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®«ßº˛£©µƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®¢Ú£©µ±ƒÍ≤˙¡øŒ™∂ý…Ÿ«ßº˛ ±£¨∏√π´Àæ‘⁄’‚“ª–¬≤˙∆∑µƒ…˙≤˙÷–À˘ªÒ¿˚»Û◊Ó¥Û.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øø’∆¯÷ ¡ø÷˜“™ ÐŒ€»æŒÔ≈≈∑≈¡øº∞¥Û∆¯¿©…¢µ»“ÚÀÿµƒ”∞œÏ£¨ƒ≥ –ª∑±£ºý≤‚’æ2014ƒÍ10‘¬¡¨–¯10ÃÏ£®¥”◊ÛµΩ”“∂‘”¶1∫≈÷¡10∫≈£©≤…ºØ∏√ –ƒ≥µÿ∆Ωæ˘∑ÁÀŸº∞ø’∆¯÷–—ıªØŒÔµƒ»’æ˘≈®∂» ˝æð£¨÷∆≥……¢µ„Õº»ÁÕºÀ˘ æ£Æ
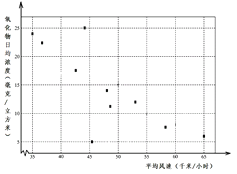
£®¢Ò£©Õ¨—ߺ◊¥”’‚10ÃÏ÷–Àʪ˙≥È»°¡¨–¯5Ãϵƒ“ª◊È ˝æ𣨺∆À„ªÿπÈ÷±œþ∑Ω≥Ã£Æ ‘«Û¡¨–¯5Ãϵƒ“ª◊È ˝æð÷–«°∫√Õ¨ ±∞¸∫¨—ıªØŒÔ»’æ˘≈®∂»◊Ó¥Û”Î◊Ó–°÷µµƒ∏≈¬ £ª
£®¢Ú£©œ÷”–30√˚—ß…˙£¨√ø»À»Œ»°5ÃÏ ˝æð£¨∂‘”¶º∆À„≥ˆ30∏ˆ≤ªÕ¨µƒªÿπÈ÷±œþ∑Ω≥ãƓ—÷™30◊È ˝æð÷–”–∞¸∫¨—ıªØŒÔ»’æ˘≈®∂»◊Ó÷µµƒ”–14◊ȣƜ÷≤…”√’‚30∏ˆªÿπÈ∑Ω≥Ã∂‘ƒ≥“ªÃÏ∆Ωæ˘∑ÁÀŸœ¬µƒ—ıªØŒÔ»’æ˘≈®∂»Ω¯––‘§≤‚£¨»Ù‘§≤‚÷µ”Î µ≤‚÷µ≤Óµƒæ¯∂‘÷µ–°”⁄2£¨‘Ú≥∆÷ÆŒ™°∞ƒ‚∫œ–ßπ˚∫√°±£¨∑Ò‘ÚŒ™°∞ƒ‚∫œ–ßπ˚≤ª∫√°±£Æ∏˘æð“‘…œ–≈œ¢ÕÍ≥…œ¬¡–2°¡2¡™±Ì£¨≤¢∑÷Œˆ «∑Ò”–95%“‘…œµƒ∞—Œ’Àµƒ‚∫œ–ßπ˚”Η°»° ˝æð «∑Ò∞¸∫¨—ıªØŒÔ»’æ˘≈®∂»◊Ó÷µ”–πÿ£Æ
‘§≤‚–ßπ˚∫√ | ƒ‚∫œ–ßπ˚≤ª∫√ | ∫œº∆ | |
˝æð”–∞¸∫¨◊Ó÷µ | 5 | ||
˝æðŒÞ∞¸∫¨◊Ó÷µ | 4 | ||
∫œº∆ |
≤Œøº ˝æð£∫
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
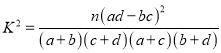 £®∆‰÷–
£®∆‰÷–![]() £©.
£©.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄÷±Ω«◊¯±Íœµ÷–£¨“‘◊¯±Í‘≠µ„![]() Œ™º´µ„£¨
Œ™º´µ„£¨ ![]() ÷·µƒ∑«∏∫∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ.“—÷™µ„
÷·µƒ∑«∏∫∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ.“—÷™µ„![]() µƒº´◊¯±ÍŒ™
µƒº´◊¯±ÍŒ™![]() £¨«˙œþ
£¨«˙œþ![]() µƒ≤Œ ˝∑Ω≥ÃŒ™
µƒ≤Œ ˝∑Ω≥ÃŒ™![]() Œ™≤Œ ˝£©.
Œ™≤Œ ˝£©.
£®1£©÷±œþ![]() π˝
π˝![]() «“”Ϋ˙œþ
«“”Ϋ˙œþ![]() œý«–£¨«Û÷±œþ
œý«–£¨«Û÷±œþ![]() µƒº´◊¯±Í∑Ω≥ãª
µƒº´◊¯±Í∑Ω≥ãª
£®2£©µ„![]() ”ε„
”ε„![]() πÿ”⁄
πÿ”⁄![]() ÷·∂‘≥∆£¨«Û«˙œþ
÷·∂‘≥∆£¨«Û«˙œþ![]() …œµƒµ„µΩµ„
…œµƒµ„µΩµ„![]() µƒæý¿Îµƒ»°÷µ∑∂Œß.
µƒæý¿Îµƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∆Ω√ʜڡø ![]() =£®1£¨x£©£¨
=£®1£¨x£©£¨ ![]() =£®2x+3£¨©Åx£©£®x° R£©£Æ
=£®2x+3£¨©Åx£©£®x° R£©£Æ
£®1£©»Ù ![]() °Œ
°Œ ![]() £¨«Û|
£¨«Û| ![]() ©Å
©Å ![]() |
|
£®2£©»Ù ![]() ”Î
”Î ![]() º–Ω«Œ™»ÒΩ«£¨«Ûxµƒ»°÷µ∑∂Œß£Æ
º–Ω«Œ™»ÒΩ«£¨«Ûxµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f(x)£Ω2sin(2x£´¶’)(0£º¶’£º2¶–)µƒÕºœÛπ˝µ„(![]() £¨£≠2)£Æ
£¨£≠2)£Æ
£®1£©«Û¶’µƒ÷µ£ª
£®2£©»Ùf(![]() )£Ω
)£Ω![]() £¨£≠
£¨£≠![]() £º¶¡£º0£¨«Ûsin(2¶¡£≠
£º¶¡£º0£¨«Ûsin(2¶¡£≠![]() )µƒ÷µ£Æ
)µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂P©ÅABCD÷–£¨∆Ω√ÊPAD°Õ∆Ω√ÊABCD£¨AB=AD£¨°œBAD=60°„£¨E°¢F∑÷± «AP°¢ADµƒ÷–µ„£¨«Û÷§£∫ 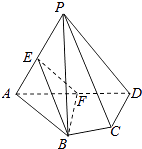
£®1£©÷±œþEF°Œ∆Ω√ÊPCD£ª
£®2£©∆Ω√ÊBEF°Õ∆Ω√ÊPAD£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬¡–√¸Ã‚÷–£¨’Ê√¸Ã‚ «£®°°°°£©
A.?x0° R£¨![]()
B.?x° R£¨![]()
C.°∞a£æ1£¨b£æ1°± «°∞ab£æ1°±µƒ≥‰“™Ãıº˛
D.…Ë![]() £¨
£¨ ![]() Œ™œÚ¡ø£¨‘Ú°∞|
Œ™œÚ¡ø£¨‘Ú°∞|![]() ?
?![]() |=|
|=|![]() ||
||![]() |°± «°∞
|°± «°∞![]() °Œ
°Œ![]() °±µƒ≥‰“™Ãıº˛
°±µƒ≥‰“™Ãıº˛
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com