练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的右焦点为，离心率为。

    （1）求椭圆的标准方程；

    （2）是椭圆上不同的三点，若直线的斜率之积为，试问从两点的横坐标之和是否为定值？若是，求出这个定值；若不是，请说明理由。

    【答案】（1）（2）两点的横坐标之和为0，详见解析

    【解析】

    （1）先由题中条件，得到，再由离心率求出，得到，进而可得椭圆方程；

    （2）设三点坐标分别为，直线的斜率分别为，得到直线的方程为：，联立直线与椭圆方程，根据韦达定理表示出与，再结合，即可得到结果.

    （1）由椭圆的右焦点得，

    又离心率得，

    所以椭圆的标准方程为：

    （2）两点的横坐标之和为0，理由如下

    设三点坐标分别为，直线的斜率分别为，

    则直线的方程为：，

    由方程组，消去得：

    ，

    ，

    故，同理可得：，

    又，即，

    从而，

    即两点的横坐标之和为常数零

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （Ⅰ）若.

    （ⅰ）求函数的极小值；

    （ⅱ）求函数在点处的切线方程.

    （Ⅱ）若函数在上有极值，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：，其焦点到准线的距离为2，直线l与抛物线C交于A，B两点，过A，B分别作抛物线C的切线，交于点M

    （Ⅰ）求抛物线C的方程

    （Ⅱ）若，求三角形面积的最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝||，实数m，n满足0＜m＜n，且f(m)＝f(n)，若f(x)在[m2，n]上的最大值为2，则＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年6月14日，世界杯足球赛在俄罗斯拉开帷幕，世界杯给俄罗斯经济带来了一定的增长，某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况，随机抽查了该商品商店某天200名顾客的消费金额情况，得到如图频率分布表：将消费顾客超过4万卢布的顾客定义为”足球迷”，消费金额不超过4万卢布的顾客定义为“非足球迷”。

    消费金额/万卢布

    合计

    顾客人数

    9

    31

    36

    44

    62

    18

    200

    （1）求这200名顾客消费金额的中位数与平均数（同一组中的消费金额用该组的中点值作代表；

    （2）该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型，采用分层抽样的方法从“非足球迷”，“足球迷”中选取5人，再从这5人中随机选取3人进行问卷调查，则选取的3人中“非足球迷”人数的分布列和数学期望。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“大众创业，万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.共生产企业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据，如表所示：

    试销单价（元）

    4

    5

    6

    7

    8

    9

    产品销量（件）

    90

    84

    83

    80

    75

    68

    已知，.

    （1）已知变量，只有线性相关关系，求产品销量（件）关于试销单价（元）的线性回方程；

    （2）用表示用（Ⅱ）中所求的线性回归方程得到的与对应的产品销量的估计值.当销售数据对应的差的绝对值时，则将售数数称为一个“好数据”.现从6小销售数据中任取2个；求“好数据”至少有一个的概率.

    （参考公式：线性回归方程中的最小二乘估计分别为，）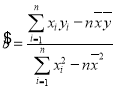

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义且为常数），若 ， .下述四个命题：

    ① 不存在极值；

    ②若函数 与函数 的图象有两个交点，则 ；

    ③若在 上是减函数，则实数 的取值范围是 ；

    ④若 ，则在的图象上存在两点，使得在这两点处的切线互相垂直

    A. ①③④B. ②③④C. ②③D. ②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法错误的是（ ）

    A.命题“若，则”的逆否命题是“若，则”

    B.“”是“”的充分不必要条件

    C.若为假命题，则、均为假命题

    D.命题：“，使得”，则非：“，”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为践行“绿水青山就是金山银山”的发展理念，某城区对辖区内，，三类行业共200个单位的生态环境治理成效进行了考核评估，考评分数达到80分及其以上的单位被称为“星级”环保单位，未达到80分的单位被称为“非星级”环保单位．现通过分层抽样的方法获得了这三类行业的20个单位，其考评分数如下：

    类行业：85，82，77，78，83，87；

    类行业：76，67，80，85，79，81；

    类行业：87，89，76，86，75，84，90，82．

    （Ⅰ）计算该城区这三类行业中每类行业的单位个数；

    （Ⅱ）若从抽取的类行业这6个单位中，再随机选取3个单位进行某项调查，求选出的这3个单位中既有“星级”环保单位，又有“非星级”环保单位的概率．

    查看答案和解析>>

    同步练习册答案