
【题目】已知圆![]() 过两点
过两点![]() ,
, ![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)直线![]() 过点
过点![]() 且与圆
且与圆![]() 有两个不同的交点
有两个不同的交点![]() ,若直线
,若直线![]() 的斜率
的斜率![]() 大于0,求
大于0,求![]() 的取值范围.
的取值范围.
【答案】(I)(x﹣1)2+y2=25 (II)(![]() ,+∞)
,+∞)
【解析】试题分析:(1)由![]() ,可得
,可得![]() 的垂直平分线方程,和已知直线方程
的垂直平分线方程,和已知直线方程
![]() 联立解得圆心坐标,再由
联立解得圆心坐标,再由![]() 求出半径,即可求得圆
求出半径,即可求得圆![]() 的标准方程;(2)设直线
的标准方程;(2)设直线![]() 的方程为:
的方程为: ![]() 即
即![]() ,设
,设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,由圆心到直线的距离小于半径列不等式,即可求得
,由圆心到直线的距离小于半径列不等式,即可求得![]() 的取值范围.
的取值范围.
试题解析:(I)MN的垂直平分线方程为:x﹣2y﹣1=0与2x﹣y﹣2=0联立解得圆心坐标为C(1,0)
R2=|CM|2=(﹣3﹣1)2+(3﹣0)2=25
∴圆C的标准方程为:(x﹣1)2+y2=25
(II)设直线![]() 的方程为:y﹣5=k(x+2)即kx﹣y+2k+5=0,设C到直线l的距离为d,
的方程为:y﹣5=k(x+2)即kx﹣y+2k+5=0,设C到直线l的距离为d,
则d=![]()
由题意:d<5
即:8k2﹣15k>0
∴k<0或k>![]()
又因为k>0
∴k的取值范围是(![]() ,+∞)
,+∞)


科目:高中数学 来源: 题型:
【题目】在三棱柱ABOA′B′O′中,∠AOB=90°,侧棱OO′⊥面OAB,OA=OB=OO′=2.若C为线段O′A的中点,在线段BB′上求一点E,使|EC|最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=sin(x﹣30°)+cos(x﹣60°),g(x)=2sin2 ![]() .
.
(1)若α为第一象限角且f(α)= ![]() ,求g(α)之值;
,求g(α)之值;
(2)求f(x﹣1080°)≥g(x)在[0,360°]内的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() )(x∈R),则下面结论错误的是( )
)(x∈R),则下面结论错误的是( )
A.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
B.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
C.函数f(x)在区间[0, ![]() ]上是增函数
]上是增函数
D.函数f(x)的图象是由函数y= ![]() sin2x的图象向右平移
sin2x的图象向右平移 ![]() 个单位而得到
个单位而得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C为圆心的圆经过点A(﹣1,0)和B(3,4),且圆心在直线x+3y﹣15=0上.
(1)求圆C的方程;
(2)设点P在圆C上,求△PAB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
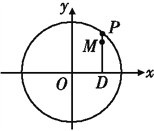
【题目】如图,设P是圆![]() 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且![]() ,
,
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为![]() 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com