Question

 [番茄花园1] 

已知定点A(－1，0)，F(2，0)，定直线l：x＝，不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E，过点F的直线交E于B、C两点，直线AB、AC分别交l于点M、N

（Ⅰ）求E的方程；

（Ⅱ）试判断以线段MN为直径的圆是否过点F，并说明理由.    

 

---

 [番茄花园1]1.

Answer 1

【答案】

 [番茄花园1] 

本小题主要考察直线、轨迹方程、双曲线等基础知识，考察平面机袭击和的思想方法及推理运算能力.

解：(1)设P(x,y)，则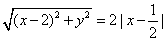

化简得x²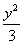－=1(y≠0)………………………………………………………………4分

(2)①当直线BC与x轴不垂直时，设BC的方程为y＝k(x－2)(k≠0)

与双曲线x²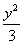－=1联立消去y得  

(3－k)²x²＋4k²x－(4k²＋3)＝0

由题意知3－k²≠0且△＞0

设B(x₁,y₁),C(x₂,y₂)，

则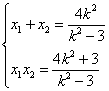

y₁y₂＝k²(x)(x)＝k²[x₁x (x₁＋x₂)＋4]

   ＝k²(＋4)

   ＝  

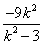
因为x₁、x₂≠－1

所以直线AB的方程为y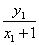＝(x＋1)

因此M点的坐标为()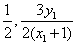

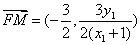,同理可得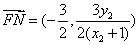  

因此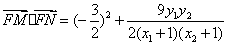

            ＝

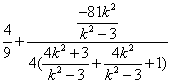
            ＝0

②当直线BC与x轴垂直时，起方程为x＝2，则B(2,3),C(2,－3)

AB的方程为y＝x＋1,因此M点的坐标为()，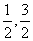

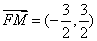
同理可得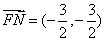

因此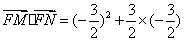＝0  

综上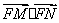＝0，即FM⊥FN

故以线段MN为直径的圆经过点F………………………………………………12分

 

 

---

 [番茄花园1]20.