练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    用反证法证明命题“”,其反设正确的是(    )
    A．B．
    C．D．
    B  

    试题分析：反证法就是从反论题入手，把命题结论的否定当作条件。所以，用反证法证明命题“”,其反设正确的是“”，选B。
    点评：简单题，反证法就是从反论题入手，把命题结论的否定当作条件，使之得到与条件相矛盾，肯定了命题的结论，从而使命题获得了证明。在应用反证法证题时，一定要用到“反设”，否则就不是反证法。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    用反证法证明：如果x>，那么x2＋2x－1≠0.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    用反证法证明命题“三角形的内角至多有一个钝角”时，假设正确的是（ ）
    A．假设至少有一个钝角B．假设至少有两个钝角
    C．假设没有一个钝角D．假设没有一个钝角或至少有两个钝角

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若P=+，Q=+（a≥0），则P，Q的大小关系是（　　）
    A．P＞QB．P=QC．P＜QD．由a的取值确定

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

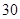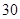    对于个互异的实数，可以排成行列的矩形数阵，右图所示的行列的矩形数阵就是其中之一．将个互异的实数排成行列的矩形数阵后，把每行中最大的数选出，记为，并设其中最小的数为；把每列中最小的数选出，记为，并设其中最大的数为.

    两位同学通过各自的探究，分别得出两个结论如下：
    ①和必相等；       ②和可能相等；
    ③可能大于；       ④可能大于．
    以上四个结论中，正确结论的序号是__________________（请写出所有正确结论的序号）．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    求证：(1);  (2) +>+。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    甲、乙、丙、丁四位歌手参加比赛，只有其中一位获奖．有人走访了四位歌手，甲说：“是乙或丙获奖．”乙说：“甲、丙都未获奖．”丙说：“我获奖了．”丁说：“是乙获奖．”四位歌手的话只有两句是对的，则获奖的歌手是(   )
    A．甲B．乙C．丙D．丁

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    用反证法证明：“”，应假设为_____________ ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知

    查看答案和解析>>

    同步练习册答案