
(1)求证fn(x)≥nx;
(2)设![]() ,求证0<x0<1;
,求证0<x0<1;
(3)是否存在区间[a,b)![]() (-∞,0],使函数h(x)=f3(x)-f2(x)在区间[a,b)的值域为[ka,kb]?若存在,求出最小的A的值及相应的区间[a,b].
(-∞,0],使函数h(x)=f3(x)-f2(x)在区间[a,b)的值域为[ka,kb]?若存在,求出最小的A的值及相应的区间[a,b].
解:(1)令g(x)=fn(x)-nx=(1+x)n-1-nx
∵g′(x)=n(x+1)n-1=n[(x+1)n-1-1]
当-2<x≤0时,g′(x)≤0;
当x>0时,g′(x)>0.
∴g(x)在(-2,0]上递减,在(0,+∞)上递增
则x=0时,g(x)min=g(0)=0
∴g(x)≥g(x)min=0
即fn(x)≥nx
(2)∵![]()
即![]()
∴x0=![]() 易得x0>0
易得x0>0
而x0-1=![]()
由(1)知x>0时,(1+x)n>1+nx
故2n+1=(1+1)n+1>n+2
∴x0<1 综上 0<x0<1.
(3)∵h(x)=f3(x)-f2(x)=x(1+x)2
h′(x)=(1+x)2+x·2(1+x)=(1+x)(1+3x)
令h′(x)=0![]() x=-1或-
x=-1或-![]()
∴h′(x)在(-2,-1)及(-![]() ,+∞)为正,
,+∞)为正,
在∵(-1,-![]() )时为负值,作图如图所示
)时为负值,作图如图所示
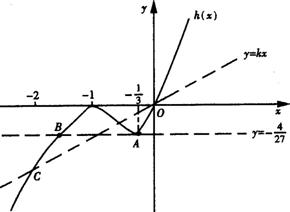
考查直线y=kx(k>0)与曲线y=h(x)相交问题假设存在k满足题意
∵在[-1,0]上,A(![]() ]为极小值点B(
]为极小值点B(![]() )
)
当y=kx绕原点O顺时针旋转到B点时
kmin=![]() 此时[a,b]=[
此时[a,b]=[![]() ,0].
,0].


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f | ′ n |
| ||
|
| fn(1) |
| fn+1(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:fn(x)≥nx.
(2)是否存在区间[a,0](a<0),使函数n(x)=f3(x)-f2(x)在区间[a,0]上的值域为[ka,0]?若存在,求出最小的k值及相应的区间[a,0];若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com