
【题目】某纺织厂为了生产一种高端布料,准备从![]() 农场购进一批优质棉花,厂方技术人员从
农场购进一批优质棉花,厂方技术人员从![]() 农场存储的优质棉花中随机抽取了
农场存储的优质棉花中随机抽取了![]() 处棉花,分别测量了其纤维长度(单位:
处棉花,分别测量了其纤维长度(单位:![]() )的均值,收集到
)的均值,收集到![]() 个样本数据,并制成如下频数分布表:
个样本数据,并制成如下频数分布表:

(1)求这![]() 个样本数据的平均数和样本方差(同一组数据用该区间的中点值作代表);
个样本数据的平均数和样本方差(同一组数据用该区间的中点值作代表);
(2)将收集到的数据绘制成直方图可以认为这批棉花的纤维长度服从分布![]() ,其中
,其中![]() .
.
①利用正态分布,求![]() ;
;
②纺织厂将![]() 农场送来的这批优质棉进行二次检验,从中随机抽取
农场送来的这批优质棉进行二次检验,从中随机抽取![]() 处测量其纤维均值
处测量其纤维均值![]() ,数据如下:
,数据如下:

若![]() 个样本中纤维均值
个样本中纤维均值![]() 的频率不低于①中
的频率不低于①中![]() ,即可判断该批优质棉花合格,否则认为农场运送是掺杂了次品,判断该批棉花不合格.按照此依据判断
,即可判断该批优质棉花合格,否则认为农场运送是掺杂了次品,判断该批棉花不合格.按照此依据判断![]() 农场送来的这批棉花是否为合格的优质棉花,并说明理由.
农场送来的这批棉花是否为合格的优质棉花,并说明理由.
附:若![]() ,则
,则![]()
![]()
![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了了解校园噪音情况,学校环保协会对校园噪音值(单位:分贝)进行了![]() 天的监测,得到如下统计表:
天的监测,得到如下统计表:
噪音值(单位:分贝) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据该统计表,求这![]() 天校园噪音值的样本平均数(同一组的数据用该组组间的中点值作代表).
天校园噪音值的样本平均数(同一组的数据用该组组间的中点值作代表).
(2)根据国家声环境质量标准:“环境噪音值超过![]() 分贝,视为重度噪音污染;环境噪音值不超过
分贝,视为重度噪音污染;环境噪音值不超过![]() 分贝,视为度噪音污染.”如果把由上述统计表算得的频率视作概率,回答下列问题:
分贝,视为度噪音污染.”如果把由上述统计表算得的频率视作概率,回答下列问题:
(i)求周一到周五的五天中恰有两天校园出现重度噪音污染而其余三天都是轻度噪音污染的概率.
(ii)学校要举行为期![]() 天的“汉字听写大赛”校园选拔赛,把这
天的“汉字听写大赛”校园选拔赛,把这![]() 天校园出现的重度噪音污染天数记为
天校园出现的重度噪音污染天数记为![]() ,求
,求![]() 的分布列和方差
的分布列和方差![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表,经过进一步统计分析,发现y与x具有线性相关关系.
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(1)根据上表给出的数据,求出y与x的线性回归方程![]() ;
;
(2)利用(1)中的回归方程,当价格![]() 元/kg时,日需求量y的预测值为多少?
元/kg时,日需求量y的预测值为多少?
(参考公式:线性回归方程![]() ,其中
,其中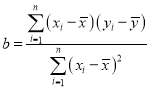 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
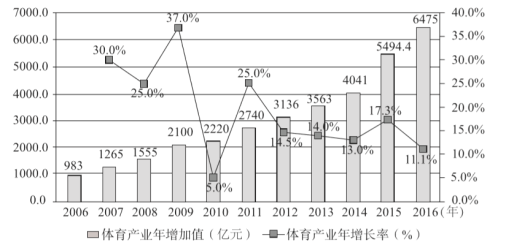
(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多![]() 亿元以上的概率;
亿元以上的概率;
(Ⅱ)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(Ⅲ)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com