
| A. | a>1 | B. | -1<a<1 | C. | -1<a<1且a≠0 | D. | a>1或a<-1 |
分析 由内函数二次函数在(-∞,-1)上为减函数,可得外函数g(t)=$lo{g}_{{a}^{2}}t$为定义域内的减函数,由此可得0<a2<1,进一步求得a的取值范围.
解答 解:∵函数t=x2-2x-3在(-∞,-1)上为减函数,
∴要使复合函数$y=lo{g}_{{a}^{2}}({x}^{2}-2x-3)$在x<-1时为增函数,
则外函数g(t)=$lo{g}_{{a}^{2}}t$为定义域内的减函数,
则0<a2<1,即-1<a<1且a≠0.
故选:C.
点评 本题考查复合函数的单调性,复合的两个函数同增则增,同减则增,一增一减则减,注意对数函数的定义域是求解的前提,考查学生发现问题解决问题的能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(b)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(a)<f(c) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 2或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
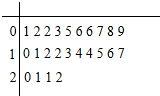 为调查了解某药物使用后病人的康复时间,从1000个使用该药的病人的康复时间中抽取了24个样本,数据如下图中的茎叶图(单位:周).专家指出康复时间在7周之内(含7周)是快效时间.
为调查了解某药物使用后病人的康复时间,从1000个使用该药的病人的康复时间中抽取了24个样本,数据如下图中的茎叶图(单位:周).专家指出康复时间在7周之内(含7周)是快效时间.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
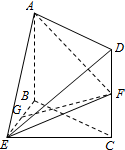 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15个 | B. | 25个 | C. | 30个 | D. | 35个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com