
【题目】在2016年8月巴西里约热内卢举办的第31届奥运会上,乒乓球比赛团体决赛实行五场三胜制,且任何一方获胜三场比赛即结束.甲、乙两个代表队最终进入决赛,根据双方排定的出场顺序及以往战绩统计分析,甲队依次派出的五位选手分别战胜对手的概率如下表:
出场顺序 | 1号 | 2号 | 3号 | 4号 | 5号 |
获胜概率 |
|
|
|
|
|
若甲队横扫对手获胜(即3∶0获胜)的概率是![]() ,比赛至少打满4场的概率为
,比赛至少打满4场的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求甲队获胜场数的分布列和数学期望.
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】现有10件产品中有3件次品,7件正品,从中抽取5件![]() 用数字表示
用数字表示![]()
(1)没有次品的抽法有多少种?
(2)有2件次品的抽法有多少种?
(3)至少1件次品的抽法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为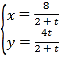 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() (
(![]() )与直线
)与直线![]() 和曲线
和曲线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱![]() 中的底面为等腰直角三角形,
中的底面为等腰直角三角形,![]() ,点
,点![]() 分别是边
分别是边![]() ,
,![]() 上动点,若直线
上动点,若直线![]() 平面
平面![]() ,点
,点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点的轨迹为
点的轨迹为![]()
![]()
A. 双曲线的一支![]() 一部分
一部分![]() B. 圆弧
B. 圆弧![]() 一部分
一部分![]()
C. 线段![]() 去掉一个端点
去掉一个端点![]() D. 抛物线的一部分
D. 抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年12月18日,作为全国首批开展空气质量新标准监测的74个城市之一,郑州市正式发布![]() 数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(
数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的
),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的![]() 的平均值为依据,播报我市的空气质量.
的平均值为依据,播报我市的空气质量.
(Ⅰ)若某日播报的![]() 为118,已知轻度污染区
为118,已知轻度污染区![]() 的平均值为74,中度污染区
的平均值为74,中度污染区![]() 的平均值为114,求重度污染区
的平均值为114,求重度污染区![]() 的平均值;
的平均值;
(Ⅱ)如图是2018年11月的30天中![]() 的分布,11月份仅有一天
的分布,11月份仅有一天![]() 在
在![]() 内.
内.
组数 | 分组 | 天数 |
第一组 |
| 3 |
第二组 |
| 4 |
第三组 |
| 4 |
第四组 |
| 6 |
第五组 |
| 5 |
第六组 |
| 4 |
第七组 |
| 3 |
第八组 |
| 1 |
①郑州市某中学利用每周日的时间进行社会实践活动,以公布的![]() 为标准,如果
为标准,如果![]() 小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
②在“创建文明城市”活动中,验收小组把郑州市的空气质量作为一个评价指标,从当月的空气质量监测数据中抽取3天的数据进行评价,设抽取到![]() 不小于180的天数为
不小于180的天数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,其中女生人数是男生人数的![]() ,男生追星的人数占男生人数的
,男生追星的人数占男生人数的![]() ,女生追星的人数占女生人数的
,女生追星的人数占女生人数的![]() .若有
.若有![]() 的把握认为是否追星和性别有关,则男生至少有( )
的把握认为是否追星和性别有关,则男生至少有( )
参考数据及公式如下:
|
|
|
|
|
|
|
|
![]()
A. 12B. 11C. 10D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二射击运动员分别对一目标射击![]() 次,甲射中的概率为
次,甲射中的概率为![]() ,乙射中的概率为
,乙射中的概率为![]() ,求:
,求:
(1)![]() 人都射中目标的概率; (2)
人都射中目标的概率; (2)![]() 人中恰有
人中恰有![]() 人射中目标的概率;
人射中目标的概率;
(3)![]() 人至少有
人至少有![]() 人射中目标的概率; (4)
人射中目标的概率; (4)![]() 人至多有
人至多有![]() 人射中目标的概率?
人射中目标的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子内有3个不同的黑球,5个不同的白球.
(1)从中取出3个黑球、4个白球排成一列且4个白球两两不相邻的排法有多少种?
(2)从中任取6个球且白球的个数不比黑球个数少的取法有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com