已知集合A={x|x2-2x-8≤0},集合B={x|x2-(2m-3)x+m2-3m≤0,m∈R},
( I)若A∩B=[2,4],求实数m的值;
( II)设全集为R,若A⊆CRB,求实数m的取值范围.
解:(Ⅰ)∵A={x|(x+2)(x-4)≤0}={x|-2≤x≤4}=[-2,4],
B={x|(x-m)(x-m+3)≤0,m∈R}={x|m-3≤x≤m}=[m-3,m]
∵A∩B=[2,4],
∴
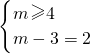
,解得m=5
( II)由(Ⅰ)知C
RB={x|x<m-3,或x>m},
∵A⊆C
RB,∴4<m-3,或-2>m,解得m<-2,或m>7.
故实数m的取值范围为(-∞,-2)∪(7,+∞)
分析:(Ⅰ)化简A=[-2,4],B=[m-3,m],根据A∩B=[-2,4],可得
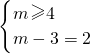
,从而求出m 的值;
(Ⅱ)根据补集的定义求出 C
RB={x|x<m-3,或x>m},由A⊆C
RB,得到4<m-3,或-2>m,由此求得实数m的取值范围.
点评:本题考查集合中参数的取值问题,补集与子集的定义,两个集合的交集的定义,属基础题.

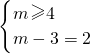 ,解得m=5
,解得m=5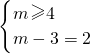 ,从而求出m 的值;
,从而求出m 的值;
