
在平面直角坐标系xOy中,O为坐标原点,A(-2,0),B(2,0),点P为动点,且直线AP与直线BP的斜率之积为- .
.
(1)求动点P的轨迹C的方程;
(2)过点D(1,0)的直线l交轨迹C于不同的两点M,N,△MON的面积是否存在最大值?若存在,求出△MON的面积的最大值及相应的直线方程;若不存在,请说明理由.
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集11讲练习卷(解析版) 题型:填空题
一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球的表面积为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷(解析版) 题型:填空题
设函数f(x)=|x+1|+|x-a|(a>0).若不等式f(x)≥5的解集为(-∞,-2]∪(3,+∞),则a的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连结CD.
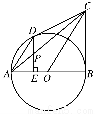
(1)求证:CD是⊙O的切线;
(2)过点D作DE⊥AB于点E,交AC于点P,求证:P点平分线段DE.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.

(1)证明:DB=DC;
(2)设圆的半径为1,BC=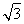 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
已知m=(2cos x+2 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调递增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f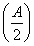 =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
已知函数f(x)=sin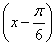 +cos
+cos ,g(x)=2sin2
,g(x)=2sin2 .
.
(1)若α是第一象限角,且f(α)=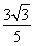 ,求g(α)的值;
,求g(α)的值;
(2)求使f(x)≥g(x)成立的x的取值集合.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(六)第二章第三节练习卷(解析版) 题型:解答题
已知函数f(x)=2|x-2|+ax(x∈R)有最小值.
(1)求实数a的取值范围.
(2)设g(x)为定义在R上的奇函数,且当x<0时,g(x)=f(x),求g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(五)第二章第二节练习卷(解析版) 题型:选择题
已知函数y=f(x)满足:对任意的x1<x2≤-1,[f(x2)-f(x1)](x2-x1)>0恒成立,则f(-2),f(- ),f(-1)的大小关系为( )
),f(-1)的大小关系为( )
(A)f(-2)<f(- )<f(-1)
)<f(-1)
(B)f(-2)>f(- )>f(-1)
)>f(-1)
(C)f(-2)>f(-1)>f(- )
)
(D)f(- )>f(-2)>f(-1)
)>f(-2)>f(-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com