Question

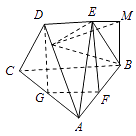
【题目】在多面体ABCDE中，BC=BA，DE∥BC，AE⊥平面BCDE，BC=2DE，F为AB的中点．

（1）求证：EF∥平面ACD；
（2）若EA=EB=CD，求二面角B﹣AD﹣E的正切值的大小．

Answer 1

【答案】
（1）证明：取AC中点G，连接DG，FG．

因为F是AB的中点，所以FG是△ABC的中位线，

则FG∥BC，FG= ，

所以FG∥DE，FG=DE，

则四边形DEFG是平行四边形，

所以EF∥DG，故EF∥平面ACD．

（2）解：过点B作BM垂直DE的延长线于点M，

因为AE⊥平面BCDE，所以AE⊥BM，则BM⊥平面ADE，

过M作MH⊥AD，垂足为H，连接BH，则AD⊥平面BMH，

所以AD⊥BH，则∠BHM是二面角B﹣AD﹣E的平面角．

设DE=a，则BC=AB=2a，

在△BEM中，EM= ，BE= ，所以BM= ．

又因为△ADE∽△MDH，

所以HM= ，则tan∠BHM= ．

【解析】（1）取AC中点G，连接DG，FG，由已知得四边形DEFG是平行四边形，由此能证明EF∥平面ACD．（2）过点B作BM垂直DE的延长线于点M，过M作MH⊥AD，垂足为H，连接BH，则∠BHM是二面角B﹣AD﹣E的平面角，由此能求出二面角B﹣AD﹣E的正切值的大小．
【考点精析】通过灵活运用直线与平面平行的判定，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行即可以解答此题．