
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:不详 题型:解答题
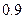 万元,汽车的维修费是第一年
万元,汽车的维修费是第一年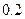 万元,以后逐年递增
万元,以后逐年递增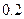 万元,问该品牌汽车使用多少年时,它的年平均费用最少?
万元,问该品牌汽车使用多少年时,它的年平均费用最少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
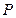 (元)与时间
(元)与时间 天的函数关系是
天的函数关系是 该商品的日销售量
该商品的日销售量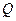 (件)与时间
(件)与时间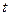 (天)的 函数关系是
(天)的 函数关系是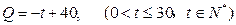 (1),求这种商品的日销售额
(1),求这种商品的日销售额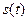 的解析式,(2)求
的解析式,(2)求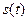 的最大值.并指出日销售额的最大时是30天中的第几天
的最大值.并指出日销售额的最大时是30天中的第几天
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式
P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式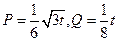 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
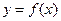 在区间
在区间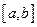 上的图像为连续不断的一条曲线,则下列说法正确的是( )
上的图像为连续不断的一条曲线,则下列说法正确的是( )A.若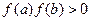 ,不存在实数 ,不存在实数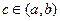 使得 使得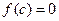 |
B.若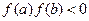 ,存在且只存在一个实数 ,存在且只存在一个实数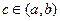 使得 使得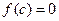 |
C.若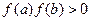 ,有可能存在实数 ,有可能存在实数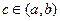 使得 使得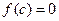 |
D.若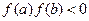 ,有可能不存在实数 ,有可能不存在实数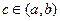 使得 使得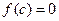 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| v | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
A.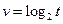 | B.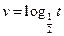 | C.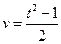 | D.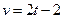 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
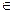 D,使得当x
D,使得当x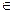 D且x>x0时,总有
D且x>x0时,总有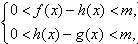 则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=
则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=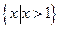 的四组函数如下:
的四组函数如下: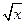 ; ②f(x)=10-x+2,g(x)=
; ②f(x)=10-x+2,g(x)= 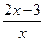 ;
;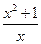 ,g(x)=
,g(x)= 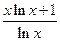 ; ④f(x)=
; ④f(x)= 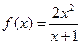 ,g(x)=2(x-1-e-x).
,g(x)=2(x-1-e-x).| A.①④ | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com