
 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1��a��b��0��$��������Ϊ$\frac{\sqrt{3}}{2}$���ҽ��㵽���ߵľ���Ϊ$\frac{\sqrt{3}}{3}$��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1��a��b��0��$��������Ϊ$\frac{\sqrt{3}}{2}$���ҽ��㵽���ߵľ���Ϊ$\frac{\sqrt{3}}{3}$������ ��1��ͨ����Բ�ҽ��㵽���ߵľ���Ϊ$\frac{\sqrt{3}}{3}$��֪$\frac{{a}^{2}}{c}$-c=$\frac{\sqrt{3}}{3}$������e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$���������a=2��c=$\sqrt{3}$�������ɵ���Բ���̣�
��2��ͨ����1����֪A��2��0����B��0��1����ֱ��ֱ��BN��AM��б�ʾ������Ҳ�Ϊ0����ͨ����ֱ��AM�ķ���Ϊx=my+2����ֱ��BN�ķ���Ϊx=-my+m�����ֱ�����Բ������������������M��$\frac{8-2{m}^{2}}{4+{m}^{2}}$��-$\frac{4m}{4+{m}^{2}}$����N��$\frac{8m}{4+{m}^{2}}$��$\frac{{m}^{2}-4}{4+{m}^{2}}$�����������㼴�ý��ۣ���ͨ����Բ���̿�ֱ֪��AB�ķ���Ϊx+2y-2=0�����������������빫ʽ�����|AB|=$\sqrt{5}$��ͨ��M��N��������������M��ֱ��AB�ľ���dM����N��ֱ��AB�ľ���dN������S=$\frac{1}{2}$|AB|��dM+dN�����㡢�����֪S=-2•$\frac{{m}^{2}+4m-4}{4+{m}^{2}}$��ͨ����f��x��=-2•$\frac{{x}^{2}+4x-4}{4+{x}^{2}}$������֪f��x�������䣨-2��$2-2\sqrt{2}$���ϵ����������ڣ�$2-2\sqrt{2}$��0���ϵ����ݼ������㼴�ý��ۣ�
��� ��1���⣺����ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1��a��b��0��$��
�������߷���Ϊ��x=$\frac{{a}^{2}}{c}$��
���ҽ��㵽���ߵľ���Ϊ$\frac{\sqrt{3}}{3}$��
��$\frac{{a}^{2}}{c}$-c=$\frac{\sqrt{3}}{3}$��
�֡�e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$��
��a=2��c=$\sqrt{3}$��
��a2=4��b2=a2-c2=4-3=1��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��2���ɣ�1����֪��A��2��0����B��0��1����ֱ��ֱ��BN��AM��б�ʾ������Ҳ�Ϊ0��
��֤������ֱ��AM�ķ���Ϊ��x=my+2����ֱ��BN�ķ���Ϊ��x=-my+m��
����$\left\{\begin{array}{l}{x=my+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$����ȥx�����ã���4+m2��y2+4my=0��
��M��$\frac{8-2{m}^{2}}{4+{m}^{2}}$��-$\frac{4m}{4+{m}^{2}}$����
����$\left\{\begin{array}{l}{x=-my+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$����ȥx�����ã���4+m2��y2-2m2y+m2-4=0��
��N��$\frac{8m}{4+{m}^{2}}$��$\frac{{m}^{2}-4}{4+{m}^{2}}$����
��ֱ��l��б��Ϊ$\frac{\frac{{m}^{2}-4}{4+{m}^{2}}+\frac{4m}{4+{m}^{2}}}{\frac{8m}{4+{m}^{2}}-\frac{8-2{m}^{2}}{4+{m}^{2}}}$=$\frac{{m}^{2}+4m-4}{2{m}^{2}+8m-8}$=$\frac{1}{2}$��
�ڽ⣺�ɣ�1����ֱ֪��AB�ķ���Ϊ��x+2y-2=0��|AB|=$\sqrt{��2-0��^{2}+��0-1��^{2}}$=$\sqrt{5}$��
�ɢٿ�֪��M��$\frac{8-2{m}^{2}}{4+{m}^{2}}$��-$\frac{4m}{4+{m}^{2}}$����N��$\frac{8m}{4+{m}^{2}}$��$\frac{{m}^{2}-4}{4+{m}^{2}}$����
�ߵ�M�ڵ�һ���ޣ�
��$\frac{1}{m}$��-$\frac{1}{2}$����-2��m��0��
���M��ֱ��AB�ľ���dM=$\frac{|\frac{8-2{m}^{2}}{4+{m}^{2}}-2•\frac{4m}{4+{m}^{2}}-2|}{\sqrt{1+4}}$=-$\frac{4{m}^{2}+8m}{\sqrt{5}��4+{m}^{2}��}$��
��N��ֱ��AB�ľ���dN=$\frac{|\frac{8m}{4+{m}^{2}}+2•\frac{{m}^{2}-4}{4+{m}^{2}}-2|}{\sqrt{1+4}}$=$\frac{16-8m}{\sqrt{5}��4+{m}^{2}��}$��
��S=$\frac{1}{2}$|AB|��dM+dN��=$\frac{\sqrt{5}}{2}$•[$\frac{16-8m}{\sqrt{5}��4+{m}^{2}��}$-$\frac{4{m}^{2}+8m}{\sqrt{5}��4+{m}^{2}��}$]
=-2•$\frac{{m}^{2}+4m-4}{4+{m}^{2}}$��
��f��x��=-2•$\frac{{x}^{2}+4x-4}{4+{x}^{2}}$������f�䣨x��=$\frac{8��{x}^{2}-4x-4��}{��4+{x}^{2}��^{2}}$=0��
��x2-4x-4=0����ã�x=$2-2\sqrt{2}$��$2+2\sqrt{2}$���ᣩ��
��f��x�������䣨-2��$2-2\sqrt{2}$���ϵ����������ڣ�$2-2\sqrt{2}$��0���ϵ����ݼ���
�֡�f��$2-2\sqrt{2}$��=-2•$\frac{��2-2\sqrt{2}��^{2}+4��2-2\sqrt{2}��-4}{4+��2-2\sqrt{2}��^{2}}$=$2\sqrt{2}$��
f��-2��=-2•$\frac{��-2��^{2}+4•��-2��-4}{4+��-2��^{2}}$=2��f��0��=-2•$\frac{0+0-4}{4}$=2��
���ı���AMBN���S��ȡֵ��Χ�ǣ���2��$2\sqrt{2}$]��
���� ������һ��ֱ����Բ���ߵ��ۺ��⣬�����������������ע����ⷽ���Ļ��ۣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
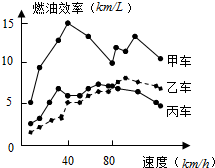 �����ġ�ȼ��Ч�ʡ���ָ����ÿ����1��������ʻ����̣���ͼ�����˼ס��ҡ������������ڲ�ͬ�ٶ��µ�ȼ��Ч�������ij���л������������80ǧ��/Сʱ����ͬ�����£��üס��ҡ������������ڸ�����ʻ����ʡ���ǣ�������
�����ġ�ȼ��Ч�ʡ���ָ����ÿ����1��������ʻ����̣���ͼ�����˼ס��ҡ������������ڲ�ͬ�ٶ��µ�ȼ��Ч�������ij���л������������80ǧ��/Сʱ����ͬ�����£��üס��ҡ������������ڸ�����ʻ����ʡ���ǣ�������| A�� | �׳� | B�� | �ҳ� | C�� | ���� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{{a^2}+{b^2}}}{2}��{��\frac{a+b}{2}��^2}$ | B�� | $\frac{b}{a}+\frac{a}{b}��2$ | C�� | $��a+b����\frac{1}{a}+\frac{1}{b}����4$ | D�� | $\frac{|a+b|}{2}��\sqrt{\;|ab|}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com