Question

【题目】某市居民自来水收费标准如下：每户每月用水量不超过4吨时，每吨为2元；当用水量超4吨时，超过部分每吨为3元．八月甲、乙两用户共交水费元，已知甲、乙两用户月用水量分别为吨、吨．

（1）求关于的函数；

（2）若甲、乙两用户八月共交34元，分别求甲、乙两用户八月的用水量和水费．

Answer 1

【答案】（1）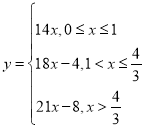

（2）甲、乙两用户八月的用水量分别为， ，水费分别为20元、14元

【解析】

（1）对甲、乙两用户用水情况分3种情况考虑，甲不超过4吨；甲超过4吨、乙不超过4吨；甲超过4吨、乙也超过4吨；从得到关于的函数表达式；

（2）由（1）得到的分段函数，讨论各段函数值为34时，从而求得，再进一步求得甲、乙各自的用水量和水费.

（1）由题意得：

①甲不超过4吨，则乙也必定不超过4吨，

所以，即时，；

②甲超过4吨、乙不超过4吨，

所以时，；

③甲超过4吨、乙也超过4吨，

所以时，．

综上所述：．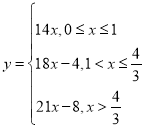

（2）当时，（舍）；

当时，（舍），

．

当时，，

甲、乙用水分别，，

设甲、乙的水费分别，．

，．

甲、乙两用户八月的用水量分别为， ，水费分别为20元、14元．