
【题目】如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB= ![]() ,AF=1,G为线段AD上的任意一点.
,AF=1,G为线段AD上的任意一点. 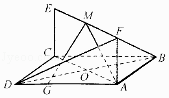
(1)若M是线段EF的中点,证明:平面AMG⊥平面BDF;
(2)若N为线段EF上任意一点,设直线AN与平面ABF,平面BDF所成角分别是α,β,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)证明:设AC∩BD=O,连结OF,OM,
由已知得AO=1,AF=1,
∴四边形AFMO是正方形,∴AM⊥OF,
又∵正方形ABCD和矩形ACEF所在平面互相垂直,交线是CA,DB⊥CA,
∴DB⊥平面ACEF,又AM平面ACEF,∴DB⊥AM,
∵BD∩OF=O,∴AM⊥平面BDF,
∵AM平面AMG,∴平面AMG⊥平面BDF
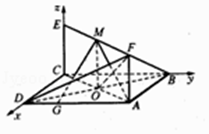
(2)解:∵正方形ABCD和矩形ACEF所在平面互相垂直,交线是CA,EC⊥CA,
∴EC⊥平面ABCD,∴CD、CB、CE两两垂直,
分别以CD、CB、CE为x,y,z轴建立坐标系,
则平面ABF的法向量 ![]() =(0,1,0),
=(0,1,0),
由(1)得平面BDF的法向量 ![]() =
= ![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,1),
,1),
由N为线段EF上任意一点,
设 ![]() =
= ![]() =
= ![]() =λ(
=λ( ![]() ),(λ∈[0,1]),
),(λ∈[0,1]),
∴ ![]() =((λ﹣1)
=((λ﹣1) ![]() ,(λ﹣1)
,(λ﹣1) ![]() ,1),
,1),
∴sinα=  =
= ![]() =
= ![]() ,
,
∵λ∈[0,1],∴ ![]() =
= ![]() =1﹣
=1﹣ ![]() ∈[0,
∈[0, ![]() ].
].
【解析】(1)设AC∩BD=O,连结OF,OM,推导出AM⊥OF,DB⊥CA,从而DB⊥平面ACEF,进而DB⊥AM,AM⊥平面BDF,由此能证明平面AMG⊥平面BDF.(2)分别以CD、CB、CE为x,y,z轴建立坐标系,利用向量法能求出 ![]() 的取值范围.
的取值范围.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】已知扇形的圆心角是α,半径为R,弧长为l.
(1)若α=75°,R=12 cm,求扇形的弧长l和面积;
(2)若扇形的周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点为原点,焦点为F(1,0),过焦点的直线与抛物线交于A,B两点,过AB的中点M作准线的垂线与抛物线交于点P,若|AB|=6,则点P的坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的高二(1)班男同学有![]() 名,女同学有
名,女同学有![]() 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个![]() 人的课外兴趣小组.
人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出![]() 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为了保护环境,发展低碳经济,某单位在政府部门的支持下,进行技术攻关,采用了新工艺,新上了把二氧化碳转化为一种可利用的化工产品的项目.经测算,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似的表示为:
(吨)之间的函数关系可以近似的表示为: ,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
(I)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(II)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共 ![]() 个,生产一个卫兵需
个,生产一个卫兵需 ![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需 ![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需 ![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过 ![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润 ![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润 ![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润 ![]() 元.
元.
(1)用每天生产的卫兵个数 ![]() 与骑兵个数
与骑兵个数 ![]() 表示每天的利润
表示每天的利润 ![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD.
(1)求证:EF∥平面PAD;
(2)若EF⊥PC,求证:平面PAB⊥平面PCD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考查两个变量![]() 和
和![]() 之间的线性关系,甲、乙两位同学各自独立作了
之间的线性关系,甲、乙两位同学各自独立作了![]() 次和
次和![]() 次试验,并且利用线性回归方法,求得回归直线分别为
次试验,并且利用线性回归方法,求得回归直线分别为![]() 、
、![]() ,已知两人得的试验数据中,变量
,已知两人得的试验数据中,变量![]() 和
和![]() 的数据的平均值都相等,且分别都是
的数据的平均值都相等,且分别都是![]() 、
、![]() ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A. 直线![]() 和
和![]() 一定有公共点
一定有公共点![]() B. 必有直线
B. 必有直线![]()
C. 直线![]() 和
和![]() 相交,但交点不一定是
相交,但交点不一定是![]() D.
D. ![]() 和
和![]() 必定重合
必定重合
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com