
分析 根据定义得出$\frac{f(2a)-f(0)}{2a}$=8a2-2a,相当于6x2-2x=8a2-2a在[0,2a]上有两个根,利用二次函数的性质解出a的范围即可
解答 解:f(x)=2x3-x2+m是[0,2a]上的“双中值函数”,
∴$\frac{f(2a)-f(0)}{2a}$=8a2-2a,
∵f'(x)=6x2-2x,
∴6x2-2x=8a2-2a在[0,2a]上有两个根,
令g(x)=6x2-2x-8a2+2a,
∴△=4+24(8a2-2a)>0,
g(0)>0,即-8a2+2a>0,
g(2a)>0,即24a2-4a-8a2+2a>0,
2a>$\frac{1}{6}$,
解得:a∈$({\frac{1}{8},\frac{1}{4}})$
故答案为:$({\frac{1}{8},\frac{1}{4}})$
点评 本题考查的知识点是根的存在性及根的个数判断,熟练掌握方程根与对应函数零点之间的关系是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
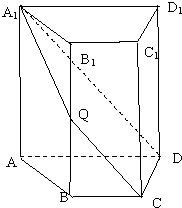 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | [3,+∞) | C. | [1,+∞) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{{{e^x}+{e^{-x}}}}{2}$ | B. | $f(x)=\frac{{{e^x}-{e^{-x}}}}{2}$ | C. | $g(x)=\frac{{{e^x}-{e^{-x}}}}{2}$ | D. | $g(x)=\frac{{{e^{-x}}-{e^x}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com